Stress results are first calculated at certain locations, called Gauss or
quadrature points, located inside each element. Simulation calculates stresses at the nodes
of each element by extrapolating the results available at the Gauss points.
After a successful run, nodal stress results at each node of every element are
available in the result database.
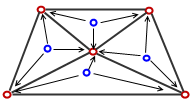 |
|
 Element nodes Element nodes
 Gauss points Gauss points
|
First order
tetrahedral elements (draft quality) have one Gauss point in their
volume. Second order tetrahedral elements have four Gauss points.
First order shell elements have one Gauss point. Second order shell
elements have three Gauss points.
For a node common to several
elements, each element gives stress results
that are slightly different. For example, if a node is common to three elements, there can be three slightly different values for every stress component at that node.
When you plot nodal
stresses, the program averages the stress values from all adjacent elements contributing to the stresses at that node.
 |
 |
| Stress values extrapolated from Gauss points to nodes of each element. |
Nodal stress values averaged at each node. |
Alternatively, you can report a single element stress value as the arithmetic
average (mean) from all Gauss points within each element. Although these stresses are
averaged between Gauss points, they are called non-averaged stresses (or element
stresses) because the averaging is done internally within the same element only.
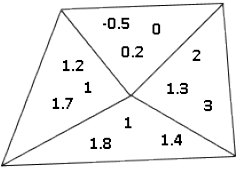 |
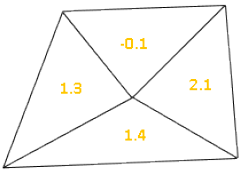 |
| These are the stress values at Gauss
points calculated by the solver. |
These are the element stress values averaged within the
element. |
Element stresses and nodal stresses are always different, but too large a
difference indicates that the mesh is not sufficiently refined in that
location.
The variation between the element and nodal stress values on an element basis is used
to estimate the energy error distribution over the whole model. Based on strain energy
principles, Simulation estimates the energy norm error for every element.
To reduce the stress errors, refine the mesh at the areas with high values of energy norm error.
Energy norm error (element) = 1 /3 * strainerror *
stresserror * (Element volume)
The strainerror is the difference between the nodal
strain and element strain on an element basis. The stresserror is the difference between the nodal stress and element stress on an
element basis.
To plot the energy norm error, in the Stress Plot PropertyManager, under Advanced Options, select Element
Values. Under Component
 , select ERR: Energy Norm Error. The energy norm error plot
is only available for static and drop test studies.
, select ERR: Energy Norm Error. The energy norm error plot
is only available for static and drop test studies.