可塑性 - von Mises 模型
降伏準則可如下式表示：
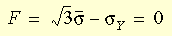
其中 s 是有效應力，sY 是從單軸向測試中得出的降伏應力。von Mises 模型可用來描述金屬的行為。使用此材料模型時，應注意下列幾項考量點：
參數RK 定義等向及動性硬化的比例。
對於純粹的等向硬化，參數 RK 有 0 的值。降伏曲面的半徑伸展，但其中心仍保持固定在偏向空間中。
對於純粹的動性硬化，參數 RK 有 1 的值。降伏曲面的半徑保持固定，但其中心可在偏向空間中移動。
可以為可塑性輸入雙線性或多線性單軸向應力-應變曲線。在雙線性應力-應變曲線定義中，可透過材料對話方塊輸入材料屬性 SIGYLD 及 ETAN。在多線性應力-應變曲線定義中，應定義應力-應變曲線。
定義應力-應變曲線時，曲線上的第一個點應為材料的降伏點。材料屬性如彈性模數 (EX)、降伏強度 (SIGYLD) 等，會於應力-應變曲線成立時從中取得，而非擷取自材料對話方塊中的材料屬性。只有 Poisson 比 (NUXY) 會從該屬性表中擷取。
落下測試研究不支援應力-應變曲線定義。
Huber-von Mises 模型可應用於實體 (粗略和精細品質) 及厚殼 (粗略和精細品質) 元素。
熱塑性不適用於薄殼元素。
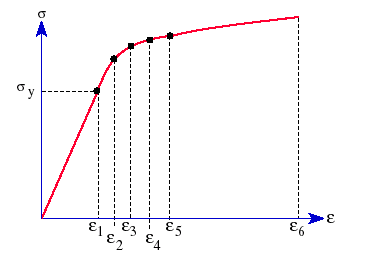
下圖描繪塑膠材料的典型應力-應變曲線：
大應變分析
在大應變可塑性理論中，將對數應變度量定義如下：
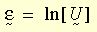
其中 U 是右拉伸張量，其通常藉由變形梯度的右極分解式 F (即 F = R U，R 是旋轉張量) 的右極分解式求出。增量對數應變的估計為：
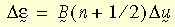
其中 B(n+1/2) 是在求解步階 n+1/2 中推算而得的應變-位移矩陣，而 Du 是增量位移向量。需注意的是，上述表達式是實際公式的二階近似法。
應力率係採用 Green-Naghdi 率，以便適當維持本構模型的架構不變性或客觀性。將應力率從整體系統轉換到 R 系統，可得：
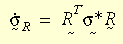
整個本構模型在形式上與小應變理論相同。大應變可塑性理論則適用於 von Mises 降伏準則、相關流動律以及等向或動性硬化 (雙線性或多線性)。雙線性硬化可支援材料屬性的溫度相依性。目前情況中使用的是徑向回歸演算法。其基本構想是藉由下式概算出正向向量：
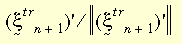
其中，
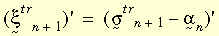
下圖描繪上述兩個方程式：
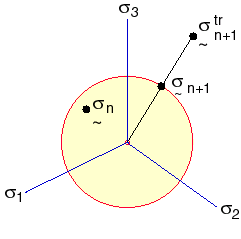
元素力向量及勁度矩陣係根據新 Lagrangian 公式計算而得。Cauchy 應力、對數應變及目前厚度 (僅限於薄殼元素) 記錄在輸出檔案中。
目前情況中的彈性是以超彈性形式加以模型化，其中假設具有小彈性應變，但允許任意的大塑性應變。對於大應變彈性問題 (橡膠類)，您可以使用超彈性材料模型來求解，例如 Mooney Rivlin。
定義多線性應力-應變曲線時應使用 Cauchy (真) 應力及對數應變。
Tresca 與 von Mises 可塑性準則之比較