조화 해석
조화 하중이나 기저 가진으로 인한 정점 상태 응답을 계산하기 위해 조화 해석을 사용합니다.
조화 하중 P의 수식은 P = A sin (w t + f)입니다. 여기에서: A는 증폭, w는 진동수, t는 시간, f는 처짐각입니다. 다른 진동수 w 의 조화 하중 및 시간에 대한 예는 아래와 같습니다:
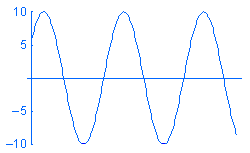

모달 시간 기록 스터디를 작성하고 시간 변화에 따른 하중을 정의할 수 있지만, 시간에 따른 순간적 응답 변화량은 필요하지 않을 수 있습니다. 이러한 경우 조화 해석을 사용하여 원하는 작용 진동수 범위에서의 정상상태 정점 응답 상태를 해결함으로써 시간과 시스템 자원을 절약할 수 있습니다. 분포 질량에 따라 모터를 대략 짐작할 수 있습니다.
예들 들어, 테스트용 테이블에 놓인 모터는 볼트를 통해 지지대 시스템에 조화 하중을 전달합니다. 지지대 시스템을 모델링하고 조화 스터디를 정의하여 작용하는 고유진동수의 모터 범위에 대한 정상상태 정점 변위, 응력 등을 계산할 수 있습니다. 분포 질량에 따라 모터를 대략 짐작할 수 있습니다.

스터디를 실행한 후, 정점 응력, 변위, 가속도, 작용 고유진동수 범위 상의 응답 처짐각 등을 볼 수 있습니다.
자세한 내용을 보려면 여기를 클릭하십시오.
감쇠 효과
이러한 해석에는 모달, Rayleigh, 복함 보드 감쇠 옵션이 있습니다.
관련 항목
조화 해석 절차
동적 해석 사용 시기
감쇠 효과
동적 해석의 하중 및 결과 옵션
선형 동적 해석 실행