Expand IntroductionIntroduction
Expand What's NewWhat's New
Expand AdministrationAdministration
Expand User InterfaceUser Interface
Expand SolidWorks FundamentalsSolidWorks Fundamentals
Expand Moving from 2D to 3DMoving from 2D to 3D
Expand AssembliesAssemblies
Expand CircuitWorksCircuitWorks
Expand ConfigurationsConfigurations
Expand Design CheckerDesign Checker
Expand Design Studies in SolidWorksDesign Studies in SolidWorks
Expand Detailing and DrawingsDetailing and Drawings
Expand DFMXpressDFMXpress
Expand DriveWorksXpressDriveWorksXpress
Expand FloXpressFloXpress
Expand Import/ExportImport/Export
Expand Mold DesignMold Design
Expand Motion StudiesMotion Studies
Expand Parts and FeaturesParts and Features
Expand PhotoView 360PhotoView 360
Expand PhotoWorksPhotoWorks
Expand RoutingRouting
Expand Sheet MetalSheet Metal
Collapse SimulationSimulation
Expand SimulationXpressSimulationXpress
Expand SketchingSketching
Expand Sustainability ProductsSustainability Products
Expand SolidWorks UtilitiesSolidWorks Utilities
Expand TolerancingTolerancing
Expand ToolboxToolbox
Expand WeldmentsWeldments
Expand Workgroup PDMWorkgroup PDM
Expand TroubleshootingTroubleshooting
Expand GlossaryGlossary
Hide Table of Contents

Harmonic Analysis

Use harmonic analysis to calculate the peak steady state response due to harmonic loads or base excitations.

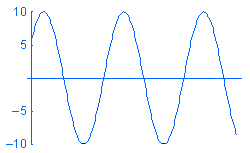
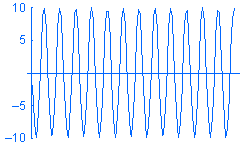
 A harmonic load P is expressed as P = A sin (w t + f) where: A is the amplitude, w is the frequency, t is time, and f is the phase angle. Sample harmonic loads of different frequencies w versus time are shown below:

Although you can create a modal time history study and define loads as functions of time, you may not be interested in the transient variation of the response with time. In such cases, you save time and resources by solving for the steady-state peak response at the desired operational frequency range using harmonic analysis. You can approximate the motor by a distributed mass.

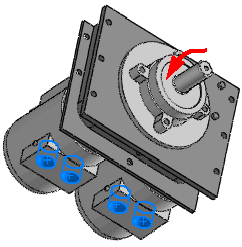
For example, a motor mounted on a test table transfers harmonic loads to the support system through the bolts. You can model the supporting system and define a harmonic study to evaluate the steady-state peak displacements, stresses, etc. for the motor’s range of operating frequencies. You can approximate the motor by a distributed mass.

After running the study, you can view peak stresses, displacements, accelerations, and velocities as well as phase angles of the response over the range of operating frequencies.

Click here for more information.

Damping effects

Modal, Rayleigh, and Composite modal damping options are available for this type of analysis.

Related Topics

Harmonic Analysis Procedure

When to Use Dynamic Analysis

Damping Effects

Loads and Result Options for Dynamic Analysis

Performing Linear Dynamic Analysis



Provide feedback on this topic

SOLIDWORKS welcomes your feedback concerning the presentation, accuracy, and thoroughness of the documentation. Use the form below to send your comments and suggestions about this topic directly to our documentation team. The documentation team cannot answer technical support questions. Click here for information about technical support.

* Required

 
*Email:  
Subject:   Feedback on Help Topics
Page:   Harmonic Analysis
*Comment:  
*   I acknowledge I have read and I hereby accept the privacy policy under which my Personal Data will be used by Dassault Systèmes

Print Topic

Select the scope of content to print:

x

We have detected you are using a browser version older than Internet Explorer 7. For optimized display, we suggest upgrading your browser to Internet Explorer 7 or newer.

 Never show this message again
x

Web Help Content Version: SOLIDWORKS 2010 SP05

To disable Web help from within SOLIDWORKS and use local help instead, click Help > Use SOLIDWORKS Web Help.

To report problems encountered with the Web help interface and search, contact your local support representative. To provide feedback on individual help topics, use the “Feedback on this topic” link on the individual topic page.

0.20.46