Modèle de matériau Nitinol
Les alliages à mémoire de forme (SMA), le Nitinol par exemple, présentent
l'effet superélastique. Le terme superélastique décrit les matériaux qui
peuvent subir de grandes déformations au cours des cycles de chargement-déchargement
sans présenter des déformations permanentes. En fait, au cours des cycles
de chargement-déchargement, le matériau présente, même pour des déformations
de 10-15 %, une réponse hystérétique, autrement dit, un chemin rigide-souple-rigide
aussi bien pour le chargement que pour le déchargement, sans aucune déformation
permanente.
Le modèle de matériau Nitinol est disponible pour les éléments volumiques
et coque.
|
|
|
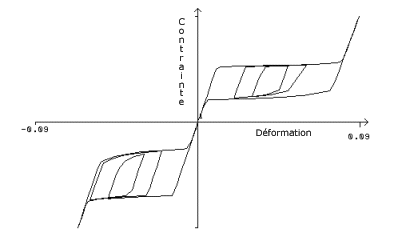
Une réponse contrainte-déformation
type pour une barre de Nitinol soumise à des conditions de chargement
uniaxial. Le matériau a un comportement différent dans des conditions
de tension et de compression |
La courbe contrainte-déformation des alliages à mémoire de forme traduit
un comportement macroscopique caractéristique, absent des matériaux traditionnels.
Ce comportement est imputable à la macromécanique sous-jacente.
Les alliages à mémoire de forme présentent des transformations de phases
martensitiques inversables, autrement dit, des transformations de type
volume-diffusion volumique-moins entre une phase en direction crystallographique
plus (« austénite ») et une phase en direction crystallographique
moins (« martensite »).
Les portions souples de la courbe de réponse représentent les zones
dans lesquelles une transformation de phase : conversion austénite en
martensite (chargement) et martensite en austénite (déchargement) se produit.
Par mesure de simplicité, cependant, nous allons utiliser le terme «
plastique » pour le comportement souple de la réponse et le terme « élastique
» pour les portions rigides.
Conformément à cette définition, le matériau présente d'abord un comportement
élastique jusqu'à ce qu'un niveau de contrainte spécifique soit atteint
(la limite d'élasticité initiale pendant le chargement). Si le chargement
se poursuit, le matériau présente un comportement élastoplastique jusqu'à
ce que la déformation plastique atteigne sa valeur de rupture. A partir
de ce point, le matériau présente de nouveau un comportement élastique
sous l'effet de chargements accrus.
Pour le déchargement, le matériau commence une nouvelle fois par présenter
un comportement élastique jusqu'à ce que la valeur de la contrainte soit
ramenée à la limite d'élasticité initiale pendant le déchargement. Le
matériau va alors poursuivre le déchargement selon un comportement élastoplastique
jusqu'à ce que toute la déformation plastique accumulée (à partir de la
phase de chargement) soit perdue. A partir de ce point, le matériau va
se décharger selon un comportement élastique jusqu'à ce qu'il reprenne
sa forme d'origine (aucune déformation permanente), sans aucune contrainte
sous des chargements nuls.
La formulation du modèle Nitinol
Puisque l'emploi de Nitinol se justifie normalement par sa résistance
à des déformations finies, ce modèle repose sur la théorie de grande déformation
combinant les déformations logarithmiques et la formulation lagrangienne
actualisée.
Le modèle constitutif est donc construit sur la base des déformations
logarithmiques et des composantes de contrainte de Kirchhoff. Cependant,
la matrice constitutive et le vecteur de contrainte sont en fin de compte
transformés pour présenter les (vraies) contraintes de Cauchy.
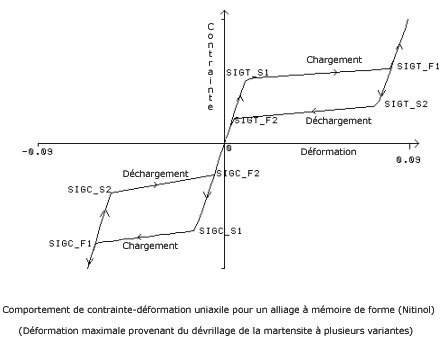
sst1, sft1 = Limite
d'élasticité initiale et finale pour le chargement de traction. [SIGT_S1,
SIGT_F1]
sst2, sft2 = Limite
d'élasticité initiale et finale pour le déchargement de traction. [SIGT_S2,
SIGT_F2]
ssc1, sfc1 = Limite
d'élasticité initiale et finale pour le chargement de compression. [SIGC_S1,
SIGC_F1]
ssc2, sfc2 = Limite
d'élasticité initiale et finale pour le déchargement de compression. [SIGC_S2,
SIGC_F2]
eul =
(Déformation plastique maximum en traction)(3/2)0,5
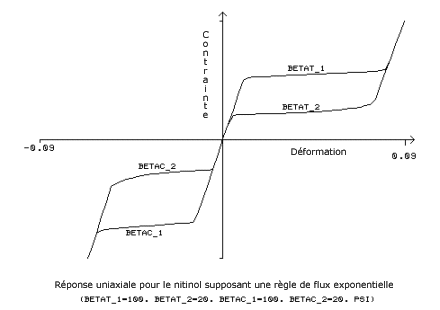
La règle de flux exponentielle utilise les contraintes d'entrée supplémentaires,
bt1, bt2, bc1, bc2 :
bt1 = paramètre
de matériau, permettant de mesurer la vitesse de transformation pour le
chargement de traction, [BETAT_1]
bt2 = paramètre
de matériau, permettant de mesurer la vitesse de transformation pour le
déchargement de traction, [BETAT_2]
bc1 = paramètre
de matériau, permettant de mesurer la vitesse de transformation pour le
chargement de compression, [BETAC_1]
bc2 = paramètre
de matériau, permettant de mesurer la vitesse de transformation pour le
déchargement de compression, [BETAC_2]
Le critère d'élasticité
Afin de modéliser la dépendance potentielle de la pression par rapport
au temps de la transformation de phase, une fonction de chargement de
type Drucker-Prager est utilisée pour le critère d'élasticité :
F(t) = sqrt(2) s + 3 a p
F-
Rif =
0
Où :
s
= contrainte effective
p = contrainte moyenne (ou pression
hydrostatique)
a
= sqrt(2/3) ( ssc1- sst1) / ( ssc1+ sst1)
Rfi = [
sfi(sqrt (2/3) +
a
)] : i = 1 : chargement, i = 2
: déchargement
La règle de flux
Par l'adoption de la définition de déformation logarithmique, il est
possible d'exprimer correctement sous une forme découplée les composantes
déviatoriques et volumétriques des tenseurs de déformation et de contrainte,
ainsi que leurs relations.
Nous allons d'abord prendre en compte les vecteurs de déformation plastique
et élastique totale, qui seront représentés par :
ep =
eul xs (
n
+ a
m
)
ee
= e -
ep
Par conséquent, le vecteur de déformation de Kirchhoff peut être évalué
sur la base de la formule suivante :
t
= pm
+ t
p = K
( q - 3 a eulxs)
t
= 2G ( e
- eul
xs
n)
Dans les formulations ci-dessus :
eul = paramètre
scalaire représentant la déformée maximum de la déformation plastique
du matériau [EUL]
xs = paramètre
compris entre zéro et un, qui exprime la mesure de la déformation plastique
q =
déformation
volumétrique = e11 + e22 + e33
e
= vecteur de déformation déviatorique
t
= vecteur de contrainte déviatorique
n = norme de contrainte déviatorique
: t/(sqrt(2) s) ?
m
= matrice d'identité de la forme vectorielle : {1,1,1,0,0,0}T
K & G = modules d'élasticité
volumique et de cisaillement : {
K = E/[3(1-2n), G = E/[2(1+v)]}
La règle de flux linéaire dans la forme incrémentielle peut être exprimée
en conséquence :
Chargement : Dxs=
( 1,0 - xs)DF / ( F - R1f)
Déchargement : Dxs=
xs DF / ( F - R2f)
Et la règle de flux exponentielle, utilisée lorsqu'un b
non nul est défini :
Chargement : Dxs=
b1(
1,0 - xs)DF / ( F - R1f)2
Déchargement : Dxs=
b2xs DF / ( F - R2f)2
Remarques :
• En général, les alliages à mémoire de forme sont insensibles aux effets
de taux. Dans la formulation ci-dessus, le « temps » représente une pseudo
variable et sa longueur n'a aucune incidence sur la résolution.
• Toutes les équations sont présentées ici pour le chargement-déchargement
de traction, puisque les expressions similaires (avec les paramètres des
caractéristiques de compression) peuvent servir pour les conditions de
chargement-déchargement de compression.
• L'algorithme de solution incrémentielle utilise une procédure retour-correspondance
dans l'évaluation des contraintes et des équations
constitutives pour un pas de simulation. Par conséquent, la résolution
comprend deux parties. Il faut initialement calculer un état d'essai ;
puis, si l'état d'essai viole le critère de flux, un ajustement permet
de ramener les contraintes à la surface de flux.
Références :
1. Auricchio, F., "A Robust Integration-Algorithm for a Finite-Strain
Shape-Memory-Alloy Superelastic Model," International Journal of
Plasticity, vol. 17, pp. 971-990, 2001.
2. Auricchio, F., Taylor,
R.L., and Lubliner, J., "Shape-Memory-Alloys : Macromodeling and Numerical
Simulations of the Superelastic Behavior," Computer
Methods in Applied Mechanics and Engineering, vol. 146, pp. 281-312, 1997.
3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. "On Large Strain
Elasto-Plastic and Creep Analysis," Finite
Elements Methods for Nonlinear Problems, Springer-Verlag 1985.
4. Hughes, T., eds. "Numerical Implementation of Constitutive Models :
Rate-Independent Deviatoric Plasticity," Theoretical
Foundation for Large-Scale Computations for Nonlinear Material Behavior,
Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.