Hyperelastisches Mooney-Rivlin-Modell
Die Mooney-Rivlin Dehnungsenergiedichte-Funktion wird wie folgt ausgedrückt:
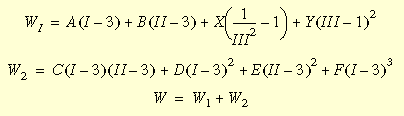
wobei I, II und III die Invarianten des rechten Cauchy-Green Verformungstensors sind und als Hauptdehnverhältnisse ausgedrückt werden können; A, B, C, D, E und F sind Mooney Materialkonstanten
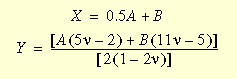
Es muss beachtet werden, dass, wenn die Materialien die Komprimierungsgrenze erreichen, die dritte Invariante (III) Einheit erreicht, während Y gegen Unendlich zunimmt. Daher bleibt für die Werte der Poissonschen Zahl in der Nähe von 0,5 der letzte Eintrag in w1 gebunden und eine Lösung kann erhalten werden.
Das Mooney-Rivlin-Materialmodell kann mit Volumenkörperelementen und dickwandigen Schalen verwendet werden. Die Materialeigenschaften für das Mooney-Rivlin-Modell werden in das Dialogfeld Material eingegeben. Es können bis zu sechs Mooney-Rivlin-Konstanten eingegeben werden: Mooney_A, Mooney_B, Mooney_C, Mooney_D, Mooney_E und Mooney_F.
Die Mooney-Rivin Konstanten werden automatisch berechnet, wenn die Option Kurvendaten zur Berechnung der Materialkonstanten verwenden im Dialogfeld Material aktiviert ist. Die Konstanten werden im aktiven Ergebnisordner der Studie in einer Textdatei mit der Erweiterung .log gespeichert.
ANMERKUNGEN
Verwenden Sie die iterative NR (Newton-Raphson)-Methode.
Werte der Poissonschen Zahl von größer oder gleich 0,48 aber kleiner als 0,5 sind zulässig. Wenn die Verschiebungs-Druck-Formel verwendet wird, sollte die Poissonsche Zahl zwischen 0,499 und 0,4999 liegen.
Gummiartige Materialien verformen sich in der Regel bei geringen Lasten sehr schnell und erfordern daher eine langsame anfängliche Belastung.
Bei der Arbeit mit gummiartigen Materialien wird ein schneller Belastungsanstieg aufgrund des stark nicht-linearen Verhaltens häufig zu numerischer Instabilität (negative diagonale Ausdrücke bei der Steifigkeit) oder Divergenz während Gleichgewichtsiterationen führen. Der automatische, adaptive Stufenalgorithmus kann in solchen Fällen hilfreich sein.
Die Verschiebung der Bogenlängensteuerung kann effektiver sein als Kraftsteuerung, sofern negative diagonale Angaben unter verschiedenem Belastungsausmaß wiederholt auftreten.
Bei starken Schalenelementen vereinfacht sich die Analyse, da Komprimierfestigkeit nicht zu ungebundenen Ausdrücken führt. Die Formel wird unter der Annahme abgeleitet, dass perfekte Komprimierfestigkeit (Poissonsche Zahl 0,5) vorhanden ist, und daher wird NUXY vernachlässigt.
Die Konstanten A und B müssen so definiert werden, dass (A+B) > 0 gilt. Weitere Informationen zur Bestimmung der Werte der Konstanten A und B finden Sie in den Arbeiten von .
Definieren hyperelastischer Modelle...