線形等方性弾性モデル（Linear Elastic Isotropic Model）

方向によって材料の特性が変わらない場合、その材料は等方性と言います。 したがって、等方性材料は全ての方向において同じ弾性係数、ポアソン比、熱膨張係数、熱伝導率などを持っています。 等方性という用語は、時には熱膨張係数の方向を持たない材料を表すためにも使用されます。

等方性弾性特性を定義するには、弾性係数Exを定義する必要があります。  値が指定されていない場合、ポアソン比nxyとしてプログラムによって0.0 が使用されます。   ポアソン比の一般的な値は、0.3 です。 せん断弾性係数 Gxy は、明示されている場合もプログラムが関係を使用して内部算出します。

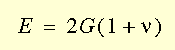
等方性材料の剛性マトリックスには、2つの独立した係数のみが含まれています。 次の章では、熱ひずみの効果を含む2次元および3次元の等方性応力-ひずみ関係を説明します。

等方性応力-ひずみ関係（Isotropic Stress-Strain Relations）

熱効果を含む等方性応力-ひずみ関係の最も一般的な形は、下図で示されているものです：

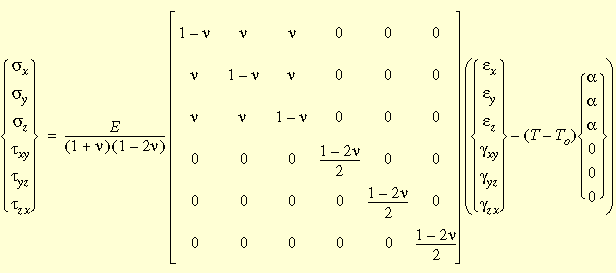
線形弾性材料モデルの仮定（Assumptions of Linear Elastic Material Models）

線形弾性材料は以下のように仮定します：

• 線形の仮定： 発生した応答値は、載荷した荷重値に比例します。 例えば、荷重の大きさを2倍にすれば、モデルの応答値（変位、ひずみ、応力など）は2倍になるということです。 以下の条件を満たしていれば、線形を仮定することができます：

• 最大応力は、応力-ひずみ曲線の原点から直線で定義される線形の範囲にあります。 応力が増加すると、部品はある応力レベル以上で非線形の動作を示します。 この仮定は、応力がこのレベル未満であるべきことを表明しています。 しかし、ゴムのように低い応力レベルでも、応力-ひずみ関係が非線形である材料には適用することができません。

• 最大変位はモデルの大きさに比べて小さい。 例えば、板の最大変位は、その板の厚さに比べ十分に小さくなければなりませんし、梁の最大変位は、その断面（例えば矩形）の小さい方の寸法より小さくなければ、線形の仮定はできないということです。

• 弾性の仮定: 荷重は永久変形を引き起こしません。 このような場合、モデルは完全に弾性であると仮定されます。 荷重が除去されると、モデルは完全に荷重載荷前の形状に戻ります。

等方性 vs. 直交異方性材料