상대 오차

모든 절점에서의 변위가 계산된 후 변형률 계산이 수행되고 각 요소에 대한 응력이 개별적으로 계산됩니다. 응력은 각 요소 내 특정 점에서 계산됩니다. 이러한 점은 정확한 계산 결과를 구하기 위해 각 요소에 의도적으로 포함되어 있으며 가우스의 점 또는 구적법 점이라고 합니다.

가우스 점에서 응력이 계산된 후 외삽법에 의해 각 요소에 대한 절점 응력이 계산됩니다.

정확한 해석 결과를 위해 모든 요소는 그 공통 절점에서 동일한 응력 값이 나와야 합니다. FEA에 의해 얻어지는 변위장은 연속적인 반면, 대개 응력장은 요소 간에 비연속적입니다. 서로 다른 요소는 대개 공통 절점에서 다른 응력 값이 나옵니다. 따라서, 각 요소에 대한 값의 평균을 내서 공통 절점에서의 절점 응력이 계산됩니다.

공통 절점에서의 응력 편차는 변형률 에너지 법칙을 기반으로 해석의 정확도 측정 기준을 제공합니다. 다음과 같이 오차 분포가 계산됩니다.

가정:

si*= 관련 요소의 공통 절점에서의 응력

s = 공통 절점에서의 평균 응력

공통 절점에서 각 요소로부터 계산된 응력 값과 평균 응력 값의 차이는 다음 수식으로 표현됩니다.

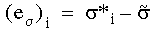
각 요소에 대한 에너지 놈(energy norm)의 오차는 다음 수식으로 계산됩니다.

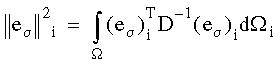
여기에서 D는 탄성 매트릭스이며 Wi는 요소 영역입니다. 전체 오차는 모든 요소의 오차를 합해 계산됩니다.

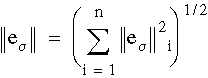
여기에서 n은 전체 요소 수입니다. 각 요소의 오차 비율은 다음 식으로 계산됩니다.

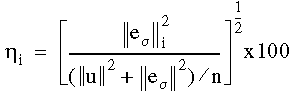
여기에서 ||u||는 다음 식으로 계산된 총 변형률 에너지의 두 배입니다.

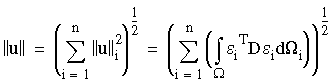
여기에서 e는 변형률 벡터입니다.

hi는 응력 플롯 PropertyManagerr에서 결과 표시 유형을 요소 응력으로, 부품을 ERR: Stress Energy로 설정할 때 플롯됩니다. 플롯되는 오차는 응력이 아닌 에너지 놈의 오차입니다. 그러나, 이 오차 플롯이 균일 메시의 상대 응력 오차 분포를 나타내기 위해 표시될 수 있습니다. 이 양은 p-adaptive 방법에 사용되어 에너지 오차가 큰 위치에서의 결과를 개선시킵니다.

오차 평가에 대한 자세한 내용은 International Journal for Numerical Methods in Engineering, vol. 24, 337-357 (1987) “A Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis” by O.C. Zienkiewicz and J. Z. Zhu)을 참조하십시오.