Нелинейная упругая модель
Для отдельного случая данных изменений напряжений в части пропорциональной нагрузки с плавными изменениями, находящихся в постоянном взаимном соотношении компонентов тензора напряжения, деформации могут быть выражены в виде конечного состояния напряжения, в следующем формате:
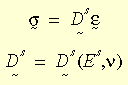
где Ds - секущая матрица материала, Es - секущий модуль и n -коэффициент Пуассона. Для использования данной модели, должны быть определены NUXY коэффициента Пуассона и диаграмма напряжения-деформации материала.
Вектор суммарной деформации e используется, для расчета эффективной деформации e, с целью получения секущего модуля из определенной пользователем диаграммы (напряжения-деформации) материала. Для трехмерной диаграммы,
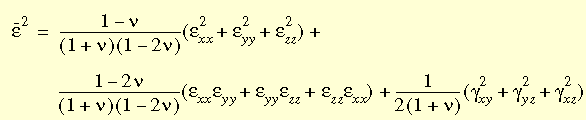
Диаграмма напряжения-деформации из третьего (сжатия) к первому (растяжения) квадранту применяются к данной модели, для двух- и трехмерных элементов с некоторыми модификациями. Для получения секущего и тангенциального модулей материала, используется метод интерполяции. Определение коэффициента R, являющегося функцией объемной деформации F, эффективной деформации и коэффициента Пуассона, R выполняется, при помощи следующего выражения:
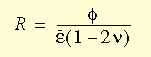
Было установлено следующее: R = 1 представляет случай неосевого растяжения, а R = -1 относится к случаю сжатия. Данные два случая установлены к верхнему и нижнему пределу, с обеспечением возврата программой значения R к установленному параметру, в случае превышения данных двух пределов. Нелинейная упругая модель материала может использоваться с твердотельными и сетками оболочек.
Ниже, представлена типовая диаграмма напряжения-деформации нелинейной модели материала: