Модель материала нитинол

Сплавы с эффектом запоминания формы, например, с материалом нитинол, обладают эффектом сверхупругости. Понятие "сверхупругости" используется для описания материалов способных подвергаться серьезным деформациям в циклическом режиме нагрузки-разгрузки, без образования постоянных деформаций. В действительности, в циклическом режиме нагрузки-разгрузки, даже при напряжениях до 10-15%, материал демонстрирует гистерезисную реакцию, с жестким-мягким-жестким поведением для циклов нагрузки и разгрузки, без постоянной деформации.

Модель с материалом нитинол представлена для твердотельных элементов и оболочек.

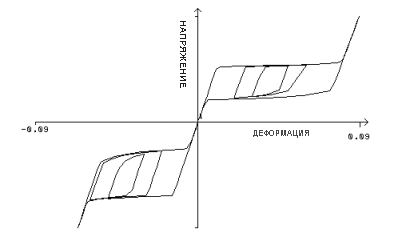
Типовая реакция напряжения-деформации для полосы нитинола, при условиях неосевой нагрузки. Примечание: материал демонстрирует различное поведение при растяжении и сжатии.

Диаграмма напряжения-деформации для сплавов с эффектом запоминания формы показывает характерное макроповедение, не отмеченное у обычных материалов. Поведение объясняется лежащими в основе материала макромеханическими характеристиками.

Сплавы с эффектом запоминания формы обладают способностями реверсивных мартенситных фазовых превращений - твердотельно-твердотельных бездиффузионных превращений между кристаллографически более (аустенит) и менее (мартенсит) упорядоченными фазами.

В мягкой части данной диаграммы реакции, представлены области происхождения фазовой трансформации превращения аустенита в мартенсит (нагрузка) и мартенсита в аустенит (разгрузка).

Однако, в целях упрощения, для обозначения поведения в мягкой части диаграммы реагирования, будет использоваться термин "пластичный", а для жестких частей - "упругий".

В соответствии с данным определением, сначала, материал показывает упругое поведение, до достижения определенного уровня напряжения (начальное напряжение текучести при нагрузке). При продолжении нагрузки, материал показывает упругопластичные характеристики, до момента достижения пластичным напряжением предельного значения. От данной точки, материал снова начинает демонстрировать упругие свойства, при увеличении нагрузок.

При разгрузке, материал всегда начинает показывать упругие свойства, до момента снижения напряжения до начального уровня напряжения текучести при разгрузке. Затем, разгрузка материала происходит с упругопластичными характеристиками, до момента полного снятия накопленных (с фазы нагрузки) пластичных напряжений. С данной точки, разгрузка материала производится с упругими свойствами, до возврата в первоначальное состояние (без постоянных деформаций), с нулевыми напряжениями при нулевых нагрузках.

Модель материала нитинол

В связи с обычным применением материала нитинол из-за способности подвергаться конечным напряжениям, для данной модели, применяется теория больших напряжений с использованием логарифмических напряжений вместе с обновленной формулировкой Лагранжа.

Следовательно, модель состояния создается, для отображения отношения логарифмических напряжений и компонентов напряжения Кирхгофа. Однако, в конечном счете, матрица состояния и вектор напряжения трансформируются, для представления напряжений Коши (истинных).

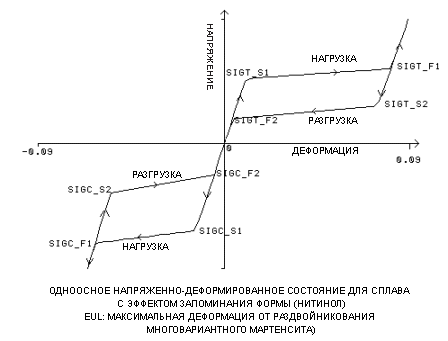
sst1, sft1=начальный и конечный пределы текучести для нагрузки растяжения. [SIGT_S1, SIGT_F1]

sst2, sft2=начальный и конечный пределы текучести для разгрузки растяжения.. [SIGT_S2, SIGT_F2]

ssc1, sfc1=начальный и конечный пределы текучести для нагрузки сжатия. [SIGC_S1, SIGC_F1]

ssc2, sfc2=начальный и конечный пределы текучести для разгрузки растяжения.. [SIGC_S2, SIGC_F2]

eul = (Предел прочности при пластичном растяжении)(3/2)0.5

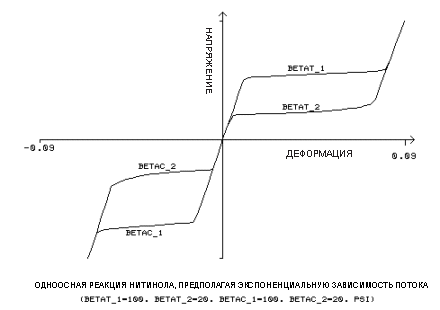
Правило экспоненциального потока использует дополнительные вводные постоянные bt1, bt2, bc1, bc2:

bt1 = параметр материала, измеряющий скорость изменения нагрузки растяжения, [BETAT_1]

bt2 = параметр материала, измеряющий скорость изменения разгрузки растяжения, [BETAT_2]

bc1 = параметр материала, измеряющий скорость изменения нагрузки сжатия, [BETAC_1]

bc2 = параметр материала, измеряющий скорость изменения разгрузки сжатия, [BETAC_2]

Критерий растяжения

Для моделирования возможности зависимости фазовых превращений от давления, используется функция нагрузки по Drucker-Prager для критерия растяжения:

 F(t) = sqrt(2) s + 3 a p

 F- Rif = 0

Где:

s = эффективное напряжение

p = среднее напряжение (или гидростатической давление)

a = sqrt(2/3) ( ssc1- sst1) / ( ssc1+ sst1)

Rfi = [ sfi(sqrt (2/3) + a )] : i = 1: нагрузка, i = 2: разгрузка

Правило потока

Благодаря принятию понятия логарифмической деформации, девиаторный и объемный компоненты тензоров деформации и напряжения, а также, связанные отношения могут быть корректно выражены в виде несвязанных уравнений.

Сначала, требуется представить векторы суммарного пластичной и упругой деформации:

ep = eul xs ( n + a m )

ee = e  - ep

В результате, может быть получен вектор напряжения Кирхгофа:

t = pm + t

p = K ( q - 3 a eulxs)

t = 2G ( e - eul xs n)

В приведенных выше формулировках:

eul = ?скалярный параметр, представляющий максимальную пластичную деформацию материала [EUL]

xs = ?параметр между 0 и 1, используемый в качестве меры пластической деформации

q =  объемная деформация = e11 + e22 + e33

e = вектор девиаторной деформации

t= вектор девиаторного напряжения

n = норма девиаторного напряжения: t/(sqrt(2) s) ?

m = единичная матрица в векторной форме: {1,1,1,0,0,0}T

K и G = модули для сыпучих материалов и упругого сдвига: { K = E/[3(1-2n), G = E/[2(1+v)]}

Соответствующим образом, может быть выражено правило линейного потока в возрастающем виде:

Загрузка: Dxs= ( 1,0 - xs)DF / ( F - R1f)

Разгрузка Dxs= xs DF / ( F - R2f)

Также, правило экспоненциального потока, используемое при назначении b, отличного от 0:

Загрузка: Dxs= b1( 1,0 - xs)DF / ( F - R1f)2

Разгрузка Dxs= b2xs DF / ( F - R2f)2

Примечания:

• В основном, сплавы с эффектом запоминания формы считаются нечувствительным к связанным со скоростью эффектам. Следовательно, приведенная выше формулировка "времени" представляет псевдо-переменную, длина которой не оказывает воздействия на решение.

• Все представленные уравнения относятся к нагрузке-разгрузке растяжения, в связи с возможностью использования подобных выражений (с параметрами свойств сжатия) для условий нагрузки-разгрузки сжатия.

• Представленный возрастающий алгоритм решения использует методику отображения последования, в оценке напряжений, и  уравнения состояния, для шага решения. Соответственно, решение состоит из двух частей. Сначала, производится вычисление пробного состояния; затем, при нарушении критерия потока пробным состоянием, выполняется регулировка для приведения напряжений к поверхности потока

Справочные документы:

1. Auricchio, F., “A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model,” International Journal of Plasticity, vol. 17, pp. 971-990, 2001.

2. Auricchio, F.,  Taylor, R.L., and Lubliner, J., “Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior”, Computer Methods in Applied Mechanics and Engineering, vol. 146, pp. 281-312, 1997.

3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. “On Large Strain Elasto-Plastic and Creep Analysis,”  Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.

4. Hughes, T., eds. “Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity,”  Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.