Rayleigh Damping
The n
x n symmetric
damping matrix [C]
is formulated as a linear combination of the mass [M]
and stiffness [K]
matrices:
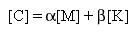(Equation 1)
The type of damping described by (Equation 1) is known as Rayleigh or
proportional damping.
This form of [C]
is orthogonal with respect to the system eigenvectors.
By applying the modal coordinate transformation,
the modal damping matrix [c] becomes
diagonal:
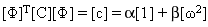(Equation
2)
You
can define Rayleigh damping for linear and nonlinear dynamic studies.
Relation of Rayleigh Coefficients
and Modal Damping Ratio
The modal damping matrix
[c] is given
by:
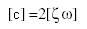(Equation 3)
The coefficient
of viscous damping ci for the ith mode is calculated by:
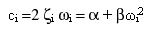(Equation
4),
and the viscous damping ratio zi
is expressed as
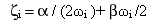(Equation 5)
If the damping ratios for the ith
and jth modes are zi and zj, then the Rayleigh coefficients
a and
b are
calculated from the solution of the two algebraic equations:
(Equation 6)
If both modes have the same damping ratio ( zi
= zj = z) , then the values of a
and b are given by:
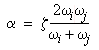(Equation 7) 
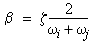(Equation 8)
The
viscous damping ratio z
for any other mode varies with frequency
as shown in the figure:
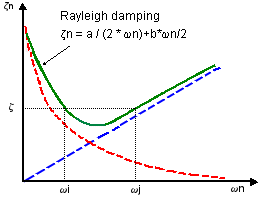
Related
topics
Global
Damping