クリープモデル(Creep Models)
クリープは、一定の応力条件下でもたらされる時間依存のひずみです。 クリープはほとんどのエンジニアリング材料で観測され、特に高温の金属、高分子プラスチック、コンクリート、ロケットモーターの固形燃料などにおいて観測されます。 クリープ効果の発生には時間がかかるため、一般的 に、動解析ではその効果は無視されます。
クリープ曲線は、ひずみと時間のグラフです。 クリープ曲線では、1次、2次、3次の3つの異なる段階に区別できます(下図を参照してください)。 通常は、1次および2次段階が考慮されます。
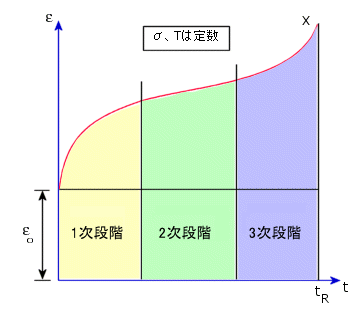
"状態方程式(Equation of State)"アプローチに基づいた2つのクリープ法則が実行されます。 各法則は単軸応力および時間の観点から単軸クリープひずみの方程式を定義します。
クリープの古典的法則(Bailey-Norton法則)(Classical Power Law for Creep (Bailey-Norton law))
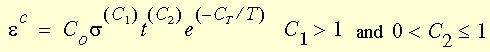
ここで、
T = 温度(K) (= 入力温度 + 参照温度 + オフセット温度)
CT = クリープの温度依存を定義する材料定数
クリープの古典的指数法則は、1つの理論式で1次および2次クリープ様式を表します。 3次クリープ様式は考慮しません。 “t"は、擬似時間ではない現在のリアルタイムです。また、sは、時間 tにおける単軸の全応力です。
これらの法則を多軸クリープ動作に拡張するために、次が仮定されます。
周期的な荷重が適用される可能性のある数値的クリープ解析ではひずみ硬化則に基づき、現在のクリープひずみ率は現在の応力およびクリープ全ひずみの関数として表されます。
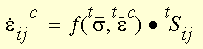
ここで、
