ニチノール材料モデル(Nitinol Material Model)
ニチノールなどの形状記憶合金(SMA)は、超弾性効果を提供します。 超弾性(Superelastic)という用語は、永久変形することなく載荷-除荷周期における大きな変位に耐えられる能力のある材料を表します。 実際に、10-15% のひずみまでの載荷-除荷周期においても、材料は載荷と除荷の両方に対して硬化-軟化-硬化パスのヒステリシス(履歴現象)反応を示し、永久変形しません。
ニチノール材料モデルは、固体とシェル要素で使用できます。
|
|
|
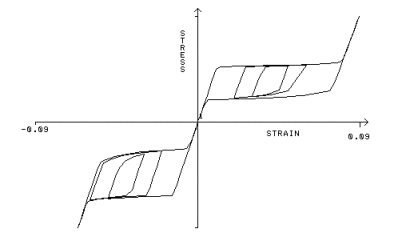
単軸荷重条件下のニチノール バーの典型的な応力-ひずみ反応。 材料は引張と圧縮では、異なる動きを見せることに注目してください。 |
形状記憶合金の応力-ひずみ曲線は、従来の材料にはない独特な巨視的動作を示します。 この動作は、基礎となるマクロ力学によるものです。
SMAは逆変態可能なマルテンサイトの相変態を示します。結晶学的に規則正しい相である「オーステナイト」と結晶学的にあまり規則正しくない相である「マルテンサイト」との相変態で原子結合の拡散がない相変態です。
応答カーブで軟化を示す領域は相変態の領域を表します。 オーステナイトからマルテンサイトへの変態(載苛)、マルテンサイトからオーステナイトへの変態(載苛)が発生します。
しかし、ここではわかりやすくするために応答カーブの軟化挙動を「弾塑性」、硬化部分を「弾性」と呼びます。
この定義によると、材料はある応力レベル(載苛の初期降伏応力)に達するまで弾性で動作します。 載苛が継続される場合、材料は塑性のひずみが応力が極限値に達するまで弾塑性の動作を示します。 この点から材料は、増加した荷重の下で再び弾性で動作します。
除荷の場合、除荷の初期の降伏応力に応力が減少するまで、材料は再び常に弾性で除荷を開始します。 次に、材料は載荷から累積された塑性のひずみがなくなるまで塑性の手法で除荷されます。 この点から材料は、永久変形のない元の形状およびゼロ荷重下のゼロ応力に戻るまで弾性で除荷されます。
ニチノール モデル方程式(The Nitinol Model Formulation)
通常、ニチノールは有限のひずみに耐えられる能力のために使用されます。そのため、このモデルには対数ひずみを利用した大ひずみ理論とともに更新ラグランジュ法が採用されます。
したがって、構成モデルは対数ひずみと Kirchhoff 応力成分を関連付けるように構成されています。 しかし、最終的に構成マトリックスおよび応力ベクトルの両方は Cauchy(真)応力を表すために変換されます。

sst1、sft1=引張載苛の初期/最大降伏応力 [SIGT_S1, SIGT_F1]
sst2、sft2=引張除苛の初期/最大降伏応力 [SIGT_S2, SIGT_F2]
ssc1、sfc1=圧縮載苛の初期/最大降伏応力 [SIGC_S1, SIGC_F1]
ssc2、sfc2=圧縮アンロードの初期/最大降伏応力 [SIGC_S2, SIGC_F2]
eul = (最大引張弾塑性ひずみ)(3/2)0.5

累乗流れ則は追加の入力定数 bt1, bt2, bc1, bc2 を使用します。
bt1 = 材料パラメータ、引張載苛の変形速度を測定、[BETAT_1]
bt2 = 材料パラメータ、引張除荷の変形速度を測定、[BETAT_2]
bc1 = 材料パラメータ、圧縮載苛の変形速度を測定、[BETAC_1]
bc2 = 材料パラメータ、圧縮除荷の変形速度を測定、[BETAC_2]
降伏判定規準(The Yield Criterion)
フェーズ変形の圧力依存の可能性をモデル化するために、降伏基準に Drucker-Prager タイプのロード関数が使用されます。
F(t) = sqrt(2) s + 3 a p
F- Rif = 0
ここで:
s = 有効応力
p = 平均応力(または、静水圧)
a = sqrt(2/3) ( ssc1- sst1) / ( ssc1+ sst1)
Rfi = [ sfi(sqrt (2/3) + a )] : i = 1: 荷重、i = 2: 除荷
流れ則
対数ひずみ定義の採用により、ひずみと応力のテンソルの偏差および容量成分とその関係は切り離された形式で正確に表すことができます。
最初に、全体的な塑性および弾性ひずみベクトルが以下のように表されると考えます。
ep = eul xs ( n + a m )
ee = e - ep
結果として、Kirchhoff応力ベクトルは以下から求められます。
t = pm + t
p = K ( q - 3 a eulxs)
t = 2G ( e - eul xs n)
上記の方程式では:
eul = 材料の最大塑性ひずみ変形を表すスカラー パラメータ[EUL]
xs = 塑性ひずみの基準となるゼロと 1 の間のパラメータ
q = 容量ひずみ = e11 + e22 + e33
e = 偏差ひずみベクトル
t= 偏差ひずみベクトル
n = 偏差応力基準: t/(sqrt(2) s) ?
m = ベクトル形式での識別マトリックス: {1,1,1,0,0,0}T
K & G = 体積せん断弾性係数: { K = E/[3(1-2n)、G = E/[2(1+v)]}
増分形式での線形の流れ則は以下のように表すことができます。
載苛: Dxs= ( 1.0 - xs)DF / ( F - R1f)
除荷: Dxs= xs DF / ( F - R2f)
そして、bがゼロ以外に定義された場合に使用する累乗流れ則:
載苛: Dxs= b1( 1.0 - xs)DF / ( F - R1f)2
除荷: Dxs= b2xs DF / ( F - R2f)2
注記:
・ 一般に、形状記憶合金は比率効果の影響を受けません。 したがって、上記公式の「時間」は擬似変数を表し、その長さは解析に影響を与えません。
・ すべての方程式は引張載荷ー除荷の例です。圧縮載荷-除荷条件の場合は、(圧縮特性パラメータを考慮した)同様の方程式を使用できます。
・ ここでの増分解法アルゴリズムは応力の評価と 解析ステップの関係方程式において回帰手法を使用します。 したがって、解法は2つの部分から構成されます。 はじめにトライアル状態が計算され、トライアル状態が流れ則の判定基準に違反する場合は応力を流れの面に戻すための調整が行なわれます。
参照文献:
1. Auricchio, F., “A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model,” International Journal of Plasticity, vol. 17, pp. 971-990, 2001.
2. Auricchio, F., Taylor, R.L., and Lubliner, J., “Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior,” Computer Methods in Applied Mechanics and Engineering, vol. 146, pp. 281-312, 1997.
3. Bergan, P.G., Bathe, K.J.およびWunderlich, eds.、 “On Large Strain Elasto-Plastic and Creep Analysis,” Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.
4. Hughes, T., eds.、 “Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity,” Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.