Expand IntroductionIntroduction
Expand AdministrationAdministration
Expand Interface utilisateurInterface utilisateur
Expand Fonctions de base de SolidWorksFonctions de base de SolidWorks
Expand Migrer de la 2D à la 3DMigrer de la 2D à la 3D
Expand AssemblagesAssemblages
Expand CircuitWorksCircuitWorks
Expand ConfigurationsConfigurations
Expand Design CheckerDesign Checker
Expand Etudes de conception dans SolidWorksEtudes de conception dans SolidWorks
Expand Mises en plan et habillageMises en plan et habillage
Expand DFMXpressDFMXpress
Expand DriveWorksXpressDriveWorksXpress
Expand FloXpressFloXpress
Expand Opérations d'import et d'exportOpérations d'import et d'export
Expand Conception à grande échelleConception à grande échelle
Expand Affichage du modèleAffichage du modèle
Expand Conception de moulesConception de moules
Expand Etudes de mouvementEtudes de mouvement
Expand Pièces et fonctionsPièces et fonctions
Expand RoutageRoutage
Expand TôlerieTôlerie
Collapse SimulationSimulation
Expand SimulationXpressSimulationXpress
Expand EsquisseEsquisse
Expand Produits SustainabilityProduits Sustainability
Expand SolidWorks UtilitiesSolidWorks Utilities
Expand TolérancementTolérancement
Expand ToolboxToolbox
Expand Constructions soudéesConstructions soudées
Expand Workgroup PDMWorkgroup PDM
Expand DépannageDépannage
Expand GlossaireGlossaire
Masquer le sommaire

Analyse harmonique

Servez-vous de l'analyse harmonique pour calculer la réponse maximale en régime permanent due à des chargements harmoniques ou des excitations de base.

Un chargement harmonique est exprimé par P = A sin (w t + f) où : A est l'amplitude, w est la fréquence, t est le temps et f est l'angle de phase. Des exemples de chargements harmoniques de fréquences différentes w en fonction du temps sont montrés ci-dessous :

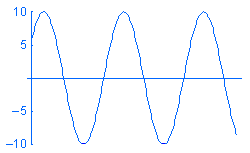
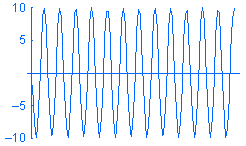
Bien que vous puissiez créer une étude modale en fonction du temps et définir les chargements comme fonctions de temps, les variations transitoires de la réponse par rapport au temps peuvent ne pas vous intéresser. Si tel est le cas, vous économiserez temps et ressources en recherchant les valeurs maximales en régime permanent pour la plage de fréquences opérationnelles souhaitée au moyen d'une analyse harmonique. Vous pouvez représenter le moteur approximativement par une masse distribuée.

Par exemple, un moteur monté sur un banc d'essai transfère des chargements harmoniques au système de support par l'intermédiaire des boulons. Vous pouvez modéliser le système de support et définir une étude harmonique pour évaluer les déplacements, contraintes, etc. maximaux en régime permanent pour la plage de fréquences opérationnelles du moteur. Vous pouvez représenter le moteur approximativement par une masse distribuée.

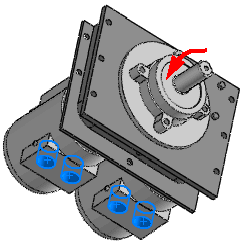
Après avoir exécuté l'étude, vous pouvez visualiser les valeurs maximales des contraintes, des déplacements, des accélérations et des vitesses ainsi que les angles de phase de la réponse sur la plage de fréquences opérationnelles.

Cliquez ici pour plus d'informations.

Effets d'amortissement

Des options d'amortissement modal, de Rayleigh et modal composite sont disponibles pour ce type d'analyse.

Rubriques connexes

Procédure d'analyse harmonique

Quand utiliser l'analyse dynamique

Effets d'amortissement

Chargements et options des résultats pour l'analyse dynamique

Effectuer une analyse dynamique linéaire



Faire un commentaire sur cette rubrique

Tous les commentaires concernant la présentation, l'exactitude et l'exhaustivité de la documentation sont les bienvenus. Utilisez le formulaire ci-dessous pour faire parvenir vos commentaires et suggestions directement à notre équipe de documentation. Celle-ci ne peut pas répondre aux questions de support technique. Cliquez ici pour des informations sur le support technique.

* Requis

 
*Courriel:  
Sujet:   Commentaires sur les rubriques d'aide
Page:   Analyse harmonique
*Commentaire:  
*   Je reconnais avoir pris connaissance et accepter par la présente la politique de confidentialité en vertu de laquelle mes données personnelles seront utilisées par Dassault Systèmes

Rubrique d'impression

Sélectionner l'étendue du contenu à imprimer :

x

La version du navigateur que vous utilisez est antérieure à Internet Explorer 7. Afin d'optimiser l'affichage, nous suggérons d'utiliser Internet Explorer 7 ou une version ultérieure.

 Ne plus afficher ce message
x

Version du contenu de l'aide sur le Web: SOLIDWORKS 2011 SP05

Pour désactiver l'aide sur le Web dans SOLIDWORKS et utiliser l'aide locale à la place, cliquez sur ? > Utiliser l'aide sur le Web de SOLIDWORKS.

Pour signaler tout problème rencontré avec l'interface ou la fonctionnalité de recherche de l'aide sur le Web, contactez votre support technique local. Pour faire part de vos commentaires sur des rubriques d'aide individuelles, utilisez le lien “Commentaires sur cette rubrique” sur la page de la rubrique concernée.

0.20.46