Amortissement de Rayleigh

La matrice d'amortissement symétrique  n x n [C] est exprimée comme une combinaison linéaire des matrices de masse [M] et de raideur [K] :

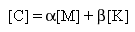(Equation 1)

Le type d'amortissement décrit par (Equation 1) est connu sous le nom d'amortissement de Rayleigh ou proportionnel.

Cette forme de [C] est orthogonale par rapport aux vecteurs propres du système.

En appliquant la transformation de coordonnées modales, la matrice d'amortissement modal [c] devient diagonale :

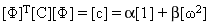(Equation 2)

Vous pouvez définir l'amortissement de Rayleigh pour les études dynamiques linéaires et non linéaires.

Relation entre les coefficients de Rayleigh et le rapport d'amortissement modal

La matrice d'amortissement modal [c] est donnée par :

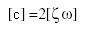(Equation 3)

Le coefficient d'amortissement visqueux ci pour le iième mode est calculé par :

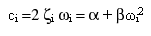(Equation 4),

et le rapport d'amortissement visqueux zis'exprime comme suit :

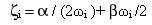(Equation 5)

Si les coefficients d'amortissement pour le iième et le jième mode sont zi et zj, alors, les coefficients de Rayleigh a et b sont calculés à partir de la solution des deux équations algébriques :

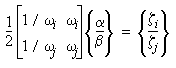(Equation 6)

Si les deux modes ont le même rapport d'amortissement ( zi= zj = z) , alors, les valeurs de a et b sont données par :

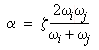(Equation 7)  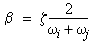 (Equation 8)

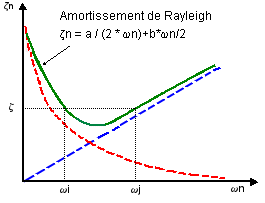
Le rapport d'amortissement visqueux z pour tout autre mode varie avec la fréquence, comme illustré dans la figure :

Rubriques connexes

Amortissement global