Matériaux isotropes et orthotropes
Matériaux isotropes
Un matériau est dit isotrope si ses propriétés mécaniques et thermiques sont identiques dans toutes les directions. Les matériaux isotropes peuvent avoir des structures microscopiques homogènes ou non homogènes. Par exemple, l'acier a un comportement isotrope mais sa structure microscopique n'est pas homogène.
Matériaux orthotropes
Un matériau est dit orthotrope si ses propriétés mécaniques ou thermiques sont différentes et indépendantes dans trois directions perpendiculaires les unes aux autres. Le bois, un grand nombre de cristaux et les métaux laminés sont des exemples de matériaux orthotropes.
Par exemple, les propriétés mécaniques du bois en un point sont décrites dans les directions longitudinale, radiale et tangentielle. L'axe longitudinal (1) est parallèle à la direction du grain (fibre). L'axe radial (2) est normal par rapport aux anneaux d'accroissement. L'axe tangentiel (3) est tangent par rapport aux anneaux d'accroissement.
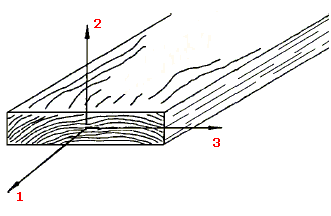
Définition des propriétés orthotropes des solides
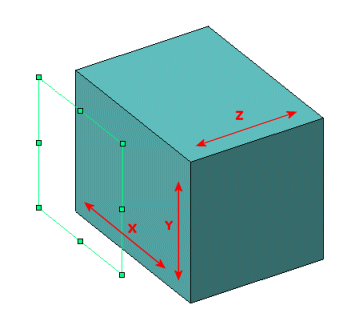
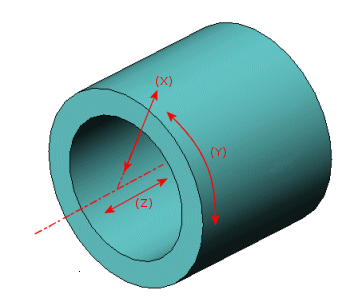
Les directions de matériaux orthotropes d'un composant sont définies à partir de la géométrie de référence sélectionnée. Si la fabrication d'une pièce fait que cela n'est pas le cas, vous devez la modéliser en plusieurs pièces pour définir correctement les directions orthotropes. Par exemple, considérez la pièce illustrée sur la figure ci-après :
Vous devez modéliser cette pièce en deux parties : le cylindre et la tôle plane. Vous pouvez ensuite utiliser comme géométrie de référence pour la définition des directions des matériaux orthotropes : un plan pour la tôle plane, et l'axe pour le cylindre.
|
|
|
|
Les directions X, Y et Z pour un matériau orthotrope lorsqu'un plan est utilisé comme géométrie de référence. |
Les directions radiale (X), tangentielle (Y) et axiale (Z) pour un matériau orthotrope lorsqu'un axe est utilisé comme géométrie de référence. |
Définition des propriétés orthotropes des coques
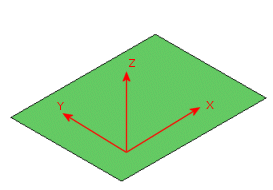
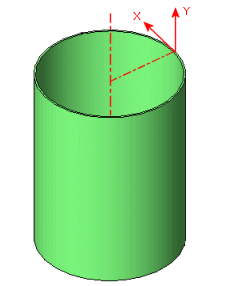
Pour une coque plane, sélectionnez un plan qui soit parallèle à la coque comme géométrie de référence. L'axe X et l'axe Y se trouvent dans le plan et l'axe Z est normal au plan. Pour une coque cylindrique, sélectionnez l'axe du cylindre comme géométrie de référence. L'axe Y est parallèle à cet axe et l'axe X lui est tangentiel.
|
|
|
|
Les directions X, Y et Z d'un matériau orthotrope pour une coque plane. |
Les directions X et Y d'un matériau orthotrope pour une coque cylindrique. |
Pour les coques composites, les directions X, Y et Z de la définition du matériau orthotrope sont différentes pour chaque pli, en fonction de l'angle de pli. La géométrie de référence n'est pas prise en compte pour la définition du matériau orthotrope.
En principe, le logiciel modifie la géométrie de référence comme suit :
Le programme transforme le système de coordonnées défini par la géométrie de référence de manière à ce que l'axe Z soit normal au plan de la coque. Le plan de la coque est défini par 3 nœuds de coin.
Si l'angle entre l'axe X de la géométrie de référence sélectionnée et la normale au plan de la coque est supérieur à 45o, le programme projette l'axe X de la géométrie de référence sur le plan de coque pour définir l'axe X modifié.
Si l'angle entre l'axe X de la géométrie de référence sélectionnée et la normale au plan de la coque est inférieur à 45o, le programme projette l'axe Y de la géométrie de référence sur le plan de coque pour définir l'axe X modifié.
L'axe Y de la géométrie de référence modifiée est ensuite défini pour compléter le système de coordonnées cartésiennes direct.
Pour définir un matériau orthotrope :