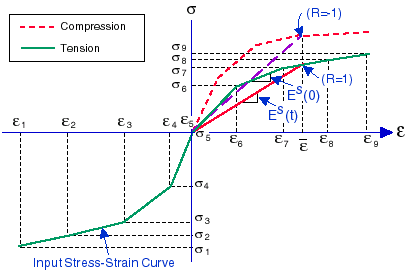
Modello elastico non lineare

Per il caso particolare della cronologia della sollecitazione in relazione a carico proporzionale, in cui i componenti di tensore di sollecitazione variano ripetitivamente a velocità costante fra loro, le deformazioni possono essere espresse in termini di stato finale di sollecitazione nella forma seguente:

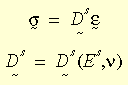
dove, Ds è la matrice del materiale secante, Es è il modulo secante e n è il coefficiente di Poisson. Per integrare questo modello, è necessario definire il valore NUXY del coefficiente di Poisson e una curva di sollecitazione-deformazione del materiale.

Viene utilizzato il vettore di sollecitazione totale e per calcolare la deformazione effettiva e per ottenere il modulo secante dalla curva di sollecitazione-deformazione del materiale definito dall'utente. Per il caso 3D,

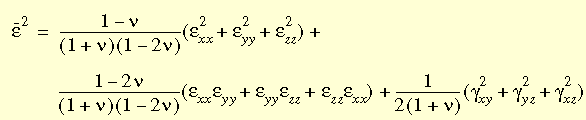
La curva di sollecitazione-deformazione dal terzo (compressione) al primo (trazione) quadrante è applicabile a questo modello per gli elementi bidimensionali e tridimensionali con qualche modifica. Viene utilizzato un metodo di interpolazione per ottenere il modulo del materiale secante e quello tangente. Definendo un rapporto R come funzione della deformazione volumetrica F, della deformazione effettiva e del coefficiente di Poisson, R ha la seguente espressione:

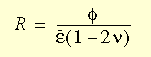
Si è osservato che R = 1 rappresenta il caso di tensione uniassiale e R = -1 rappresenta il caso di compressione. Questi due casi sono impostati come limite inferiore e limite superiore in modo che, se R supera questi valori, il software fa in modo che rientri nei limiti. È possibile utilizzare il modello dei materiali elastici non lineari con mese solide e di shell.

Di seguito viene riportata una tipica curva di sollecitazione-deformazione di un modello di materiale non lineare: