Modello di materiale in nitinol

Le leghe a memoria di forma (SMA), quali il nitinol, presentano fenomeni superelastici. Il termine superelastico è utilizzato per descrivere i materiali capaci di subire grandi deformazioni nei cicli di carico e scarico senza deformarsi permanentemente. Infatti, se il materiale viene sottoposto a cicli di carico e scarico, anche fino al 10-15% di deformazione, esso mostra una risposta isteretica, un percorso rigido-morbido-rigido sia per il carico che lo scarico, senza l'insorgere di effettive deformazioni permanenti.

Il modello del materiale Nitinol è disponibile per gli elementi solidi e di shell.

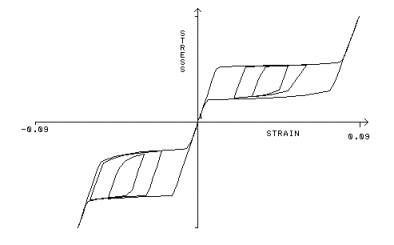
Una tipica risposta di sollecitazione-deformazione per un'asta di nitinol sottoposta a condizioni di carico uniassiale. Si noti che il materiale si comporta differentemente in tensione e compressione.

La curva sollecitazione-deformazione delle leghe SMA dimostra un chiaro comportamento macroscopico, non presente nei materiali tradizionali. Questa caratteristica è attribuita ai macromeccanismi di base.

Le leghe SMA presentano trasformazioni con fasi martensitiche reversibili, vale a dire, trasformazioni a bassa diffusione solido-solido tra una fase più ordinata rispetto alla cristallografia, "austenitica", e una meno ordinata, "martensitica".

Le parti elastiche della curva della risposta rappresentano le aree in cui si verifica una trasformazione con le seguenti fasi: una conversione di una struttura austenitica in martensitica (carico) e di una struttura martensitica in austenitica (scarico).

Tuttavia, a scopo esemplificativo, si farà riferimento al comportamento morbido della curva della risposta come "plastico" e alle parti rigide come "elastico".

In base a questa definizione, il materiale assume prima un comportamento elastico fino al raggiungimento di un determinato livello di sollecitazione (la sollecitazione di snervamento iniziale con il carico). Se il carico continua, il materiale mostra un comportamento elastoplastico finché la deformazione plastica non raggiunge il valore massimo. Da questo punto in poi, il materiale ha un comportamento elastico rispetto ai carichi aumentati.

Per lo scarico, il materiale ha sempre prima un comportamento elastico fino alla riduzione della sollecitazione alla sollecitazione di snervamento iniziale nello scarico. Il materiale, quindi, avrà un comportamento elastoplastico rispetto allo scarico finché non perde tutta la deformazione plastica accumulata. Da questo punto in poi, il materiale sottoposto allo scarico agisce elasticamente finché non ritorna alla sua forma originale (non è deformato permanentemente) con zero sollecitazioni per zero carichi.

La formula del modello in nitinol

Poiché il nitinol viene utilizzato solitamente per la sua capacità di resistenza alle deformazioni finite, per questo modello è impiegata la teoria della forte deformazione che utilizza le deformazioni logaritmiche insieme alla formula di Lagrange.

Di conseguenza, il modello costitutivo è costruito in modo da correlare le deformazioni logaritmiche ed i componenti di sollecitazione di Kirchhoff. Tuttavia, in definitiva, la matrice costitutiva e il vettore della deformazione sono entrambi trasformati per presentare le sollecitazioni di Cauchy (reali).

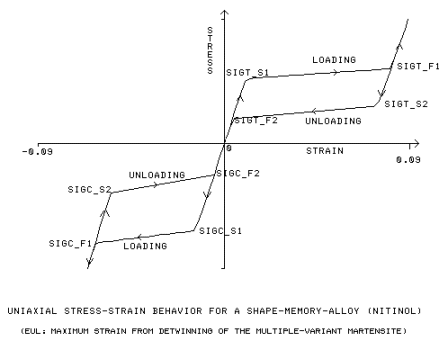
sst1, sft1= Sollecitazione di snervamento iniziale e finale per il carico di trazione. [SIGT_S1, SIGT_F1]

sst2, sft2= Sollecitazione di snervamento iniziale e finale per lo scarico di trazione. [SIGT_S2, SIGT_F2]

ssc1, sfc1= Sollecitazione di snervamento iniziale e finale per il carico di compressione. [SIGC_S1, SIGC_F1]

ssc2, sfc2= Sollecitazione di snervamento iniziale e finale per lo scarico di compressione. [SIGC_S2, SIGC_F2]

eul = (Deformazione plastica di tensione massima)(3/2)0.5

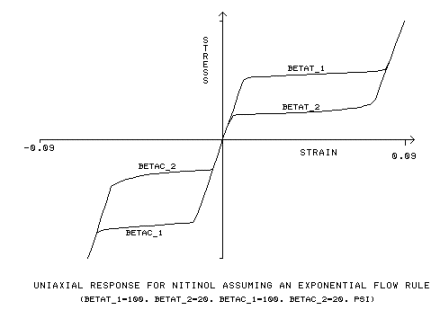
La regola di flusso esponenziale utilizza ulteriori valori costanti, bt1, bt2, bc1, bc2:

bt1 = parametro del materiale, misurazione della velocità di trasformazione per il carico di trazione, [BETAT_1]

bt2 = parametro del materiale, misurazione della velocità di trasformazione per lo scarico di trazione, [BETAT_2]

bc1 = parametro del materiale, misurazione della velocità di trasformazione per il carico di compressione, [BETAC_1]

bc2 = parametro del materiale, misurazione della velocità di trasformazione per lo scarico di compressione, [BETAC_2]

Il criterio di snervamento

Per la modellazione della possibilità della dipendenza dalla pressione di una trasformazione di fase, viene utilizzata una funzione di carico di tipo Drucker-Prager per il criterio di snervamento:

 F(t) = radq(2) s + 3 a p

 F- Rif = 0

Dove:

s = sollecitazione effettiva

p = sollecitazione media (o pressione idrostatica)

a = radq(2/3) ( ssc1- sst1) / ( ssc1+ sst1)

Rfi = [ sfi( radq (2/3) + a )] : i = 1: carico, i = 2: scarico

La regola di flusso

Attraverso l'adozione di una definizione di deformazione logaritmica, i componenti deviatorici e volumetrici dei tensori di sollecitazione e deformazione e le relative relazioni possono essere espressi correttamente in una forma di assorbimento dello shock.

Prima vengono considerati i vettori di deformazione plastica ed elastica rappresentati da:

ep = eul xs ( n + a m)

ee = e  - ep

Quindi, il vettore di sollecitazione Kirchhoff può essere calcolato come:

t = pm + t

p = K ( q - 3 a eulxs)

t = 2G ( e - eul xs n)

Nelle formule sopra riportate:

eul = parametro scalare che rappresenta la deformazione da sollecitazione plastica massima del materiale [EUL]

xs = parametro compreso tra zero e uno, come valore della deformazione plastica

q =  deformazione volumetrica = e11 + e22 + e33

e = vettore di deformazione deviatorica

t = vettore di sollecitazione deviatorica

n = norma della sollecitazione deviatorica: t/(radq(2) s)

m = matrice di identità in forma vettoriale: {1,1,1,0,0,0}T

K & G = moduli elastici di taglio e dell'ambiente circostante: { K = E/[3(1-2n), G = E/[2(1+v)]}

La regola di flusso lineare nella forma incrementale può essere espressa di conseguenza:

Carico: Dxs= ( 1.0 - xs) DF / ( F - R1f)

Scarico: Dxs= xs DF / ( F - R2f)

E la regola del flusso esponenziale, usata quando un valore b non zero è definito:

Carico: Dxs= b1 ( 1.0 - xs) DF / ( F - R1f)2

Scarico: Dxs= b2 xs DF / ( F - R2f)2

Note:

• In generale, le leghe a memoria di forma (SMA) non sono soggette a velocità. Quindi, nella formula sopra riportata il "tempo" rappresenta una pseudo variabile e la sua lunghezza non interessa la soluzione.

• Tutte le equazioni sono qui presentate per il carico/scarico di trazione, poiché espressioni simili (con parametri delle proprietà di compressione) possono essere utilizzate per le condizioni di carico/scarico di compressione.

• L'algoritmo della soluzione incrementale qui utilizza schemi di tipo "mappa di ritorno" per la valutazione delle sollecitazioni e delle equazioni costitutive  per un passo della soluzione. Di conseguenza, la soluzione è costituita da due parti. Inizialmente, viene calcolato uno stato di prova; quindi se lo stato di prova viola il criterio di flusso, vengono applicate delle modifiche affinché le sollecitazioni rientrino nella superficie di flusso.

Riferimenti:

1. Auricchio, F., "A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model", International Journal of Plasticity, vol. 17, pgg. 971-990, 2001.

2. Auricchio, F.,  Taylor, R.L., and Lubliner, J., "Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior",  Computer Methods in Applied Mechanics and Engineering, vol. 146, pgg. 281-312, 1997.

3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. "On Large Strain Elasto-Plastic and Creep Analysis",  Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.

4. Hughes, T., eds. "Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity",  Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.