Hyperelastic Mooney - Rivlin 모델
Mooney-Rivlin 변형 에너지 밀도 함수는 다음과 같습니다.
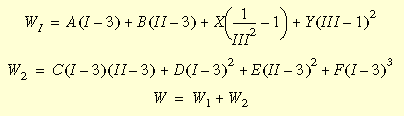
여기서 I, II, III은 오른쪽 Cauchy-Green 변형 텐서의 불변량이고 주 늘이기 비율과의 관계로 표시할 수 있습니다. A, B, C, D, E, F는 Mooney 재질 상수입니다. 그리고
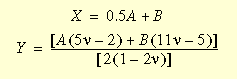
재질이 비압축률에 접근하면 세 번째 불변량 III은 항등식에 접근합니다. 여기서 Y 는 무한대로 접근합니다. 따라서 포아송비의 값이 0.5에 가까워지면 w1의 마지막 기간은 제한된 상태가 되며 솔루션이 구해집니다.
Mooney-Rivlin 재질 모델을 솔리드 요소와 두꺼운 쉘에 사용할 수 있습니다. Mooney-Rivlin 모델의 물성치는 재질 대화 상자에서 입력합니다. 최대 여섯 개의 Mooney-Rivlin 상수를 입력할 수 있습니다. Mooney_A, Mooney_B, Mooney_C, Mooney_D, Mooney_E, 및 Mooney_F.
재질 대화 상자에서 재질 불변을 계산하기 위해 곡선 데이터 사용 대화 상자가 선택되면 Mooney-Rivin 모델 상수가 자동으로 계산됩니다. 상수는 스터디의 활성 결과 폴더에 확장명이 .log인 텍스트 파일로 저장됩니다.
참고
NR(Newton-Raphson) 반복 방법을 사용하십시오.
포아송비의 값이 0.48과 0.5 미만이면 사용할 수 있습니다. 변위-압력 공식을 사용하는 경우 0.499에서 0.4999 사이의 포아송비를 사용하는 것이 좋습니다.
고무와 같은 재질은 하중이 적어도 빠르게 변형되므로 초기 부하를 천천히 가해야 합니다.
고무와 같은 재질을 처리하는 경우 상당히 비선형적으로 동작하는 문제가 있으므로 하중을 빠르게 가하면 평형 반복 중 수치가 불안정(경사도에서 음의 대각항)하거나 발산될 수 있습니다. 자동 적응 스텝 알고리즘은 이러한 경우에 도움이 될 수 있습니다.
음의 대각항이 다양한 하중률에서 반복적으로 발생하는 경우 힘 제어보다는 변위 또는 원호 길이 제어가 더 효과적임이 증명될 수 있습니다.
두께 형성이 있는 쉘 요소에서 해석은 비압축률로 인한 비결합 항이 발생하지 않으므로 단순해 집니다. 이 형성은 완전한 비압축률(포아송비 0.5)을 가정하여 파생되므로 NUXY는 무시됩니다.
상수 A 및 B는 (A+B) > 0으로 정의되어야 합니다. A와 B 상수 값을 결정하는 방법에 대한 자세한 내용은 연구 결과를 참조하십시오.
hyper 탄성 모델을 정의하는 방법...