Metody integrace

Následující metody integrace se používají pro studie nahodilé vibrace.

Standardní metoda

Standardní metoda analýzy nahodilých vibrací probíhá následovně:

1. Kolem každého požadovaného přirozeného režimu se vyberou určité frekvenční body. Umístění těchto bodů závisí na hodnotě předmagnetizačního parametru p.

Pokud má parametr hodnotu 1,0, jsou všechny frekvenční body jednotně rozloženy mezi přirozenými frekvencemi. Pokud je parametr větší než 1,0, body se vyberou blíže k přirozeným frekvencím. Výchozí hodnoty pro frekvenční body a předmagnetizační parametr jsou dány jako funkce poměru tlumení z prvního režimu. Znázornění výběru frekvenčních bodů zobrazíte klepnutím sem.

Výchozí hodnoty pro frekvenční body a předmagnetizační parametr jako funkce z jsou uvedeny níže:

Software použije výchozí hodnoty dané v tabulce 1 v případě, bsp;že je pro počet frekvenčních bodů a předmagnetizační parametr nastavena nula.

2. Modální psd odezvy se vyhodnotí u každého frekvenčního bodu. Poměr přerušení příčných kmitů (POMĚR) nastavuje omezení poměru všech možných dvojic přirozených frekvencí (w i / w j, i > j).

To znamená, že u každé dvojice režimů, kde w i / w j> POMĚR, se podmínky spektrální hustoty zanedbají. Účinky režimů se neberou v úvahu v případě, že POMĚR = 1.

2. Modální psd se potom číselně integrují v zadaném rozsahu frekvencí a tak vzniknou střední kvadratické hodnoty a kovariance modální reakce. Integrace se provede číselně pomocí Gaussovy integrace 2. nebo bsp;3. řádu v každém frekvenčním intervalu podle interpolace log-log. Střední kvadratická odezva se získá součtem shrnutí intervalů.

3. Transformací z modální na uzlové nakonec vzniknou rms posunutí, rychlosti a zrychlení systému.

Přibližná metoda

Standardní metoda integrace může zahrnovat časově náročné výpočty z důvodu číselné integrace velkých matic. Metoda přibližné integrace provádí zjednodušené řešení podle následujících předpokladů:

• Zanedbání reakce režimů, Sx(w) , která představuje vzájemný účinek režimů:

(rovnice 1)

• Psd buzení se v každém režimu považují za konstantní. Předpokládá se tedy, že každý režim je buzen „bílým šumem” se spektrální hustotou Sn, kde;

(rovnice 2)

wn je přirozená frekvence režimu n (n = 1,2,...nf).

U bílého šumu lze střední kvadratické odezvy určit analyticky pro modální odezvy:

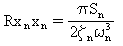(rovnice 3)

(rovnice 4)

(rovnice 5).