Definition grundlegender Größen

Die internen Kräfte eines Körpers sind an verschiedenen Stellen unterschiedlich. Auch in beliebig kleinen internen ebenen Bereichen werden Lasten von einem Teil des Körpers auf der einen Seite des Bereichs auf den Teil auf der anderen Seite ausgeübt. Spannung kennzeichnet die Intensität dieser inneren Kräfte (Kraft pro Einheitsfläche).

• Spannung. In einem zusammenhängenden Körper können Sie die Spannung an einem Punkt wie folgt berechnen:

• • Stellen Sie sich eine beliebige Ebene vor, die den Körper an diesem Punkt schneidet.

  • Bestimmen Sie eine unendlich kleine Fläche DA um diesen Punkt auf der Ebene.

  • Nehmen Sie an, dass die Kraft, die in einer bestimmten Richtung über DA übertragen wird, die Magnitude DF hat.

  • Die Spannung in dieser Richtung wird dann durch DF/DA gegeben, wenn DA sich 0 nähert.

HINWEIS: Die oben angegebenen Aktionen definieren einen Spannungs- oder Zugvektor an einem Punkt. Ein Zugvektor liefert keine eindeutige Definition des Spannungszustands an einem Punkt. Er variiert je nach beliebig gewählter Ebene. Ein Spannungstensor, beispielsweise ein echter Spannungstensor, der durch s = n.T (Matrixmultiplikation) definiert ist, wobei n den Normalenvektor der Ebene und T den Spannungs- oder Zugvektor bezeichnet, definiert die Spannung eindeutig. bsp;   

• Dehnung. Dehnung ist das Verhältnis der Änderung der Länge d L in Bezug auf die ursprüngliche Länge L. Die Dehnung ist eine dimensionslose Größe.

Reihenfolge der Berechnungen

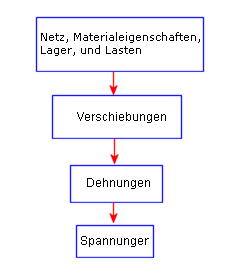
Wenn ein vernetztes Modell mit einem Satz von Verschiebungslagern und -lasten gegeben ist, geht das lineare statische Analyseprogramm wie folgt vor:

1. Das Programm erstellt und löst ein System von linearen, simultanen Finite-Elemente-Gleichgewichtsgleichungen, um die Verschiebungskomponenten an jedem Knoten zu berechnen.

2. Anschließend berechnet das Programm anhand der Verschiebungsergebnisse die Spannungskomponenten.

3. Das Programm verwendet die Dehnungsergebnisse und die Spannungs-/Dehnungsbeziehungen, um die Spannungen zu berechnen.

Spannungsberechnungen

Spannungsergebnisse werden zuerst an speziellen Punkten, so genannten Gaußschen Punkten oder Quadraturpunkten, die sich innerhalb jedes Elementes befinden, berechnet. Diese Punkte wurden ausgewählt, um optimale numerische Ergebnisse zu erzielen. Das Programm berechnet die Spannungen an den Knoten der einzelnen Elemente durch Extrapolation der an den Gaußschen Punkten verfügbaren Ergebnisse.

Nach einem erfolgreichen Durchlauf sind die Knotenspannungsergebnisse jedes Elementknotens in der Datenbank verfügbar. Knoten, die zwei oder mehreren Elementen gemeinsam sind, verfügen über mehrere Ergebnisse. Diese Ergebnisse sind im Allgemeinen nicht identisch, weil die Finite-Elemente-Methode ein Näherungsverfahren ist. Wenn z. B. drei Elemente einen gemeinsamen Knoten haben, können sich die drei Ergebnisse für die Spannungskomponente an diesem Knoten geringfügig unterscheiden.

Bei der Betrachtung der Spannungsergebnisse können Sie zwischen Elementspannungen oder Knotenspannungen auswählen. Bei der Berechnung der Elementspannungen wird der Durchschnitt der entsprechenden Knotenspannungen für jedes Element ermittelt. Bei der Berechnung der Knotenspannungen ermittelt das Programm den Durchschnittswert der entsprechenden Ergebnisse aller Elemente, die diesen Knoten gemeinsam haben.