Modello iperelastico Mooney-Rivlin

La funzione densità energia di deformazione Mooney-Rivlin è espressa come:

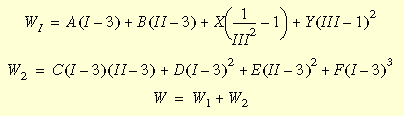
dove I, II e III sono invarianti del tensore di deformata Cauchy-Green e possono essere espresse in termini di coefficienti di trazione principale; A, B, C, D, E ed F sono costanti del materiale Mooney e

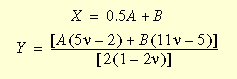
Si è osservato che quanto più il materiale si fa incomprimibile, la terza invariante III si avvicina a 1, mentre Y tende all'infinito. Quindi, per i valori del coefficiente di Poisson vicini a 0,5, l'ultimo termine in w1 rimane unito e si potrà ottenere una soluzione.

Il modello di materiali Mooney-Rivlin può essere utilizzato con elementi solidi e shell spessi. Le proprietà del materiale per il modello Mooney-Rivlin vengono specificate nella finestra di dialogo Materiale. bsp;È possibile specificare un massimo di sei costanti Mooney-Rivlin: Mooney_A, Mooney_B, Mooney_C, Mooney_D, Mooney_E e Mooney_F.

Le costanti Mooney-Rivin sono calcolate automaticamente quando l'opzione Usa i dati della curva per calcolare le costanti del materiale nella finestra Materiale è selezionata. Le costanti sono salvate in un file di testo con l'estensione .log nella cartella dei risultati attivi per lo studio.

NOTE

• Utilizzare il modello iterativo NR (Newton-Raphson).

• I valori del coefficiente di Poisson maggiori o uguali a 0,48 ma inferiori a 0,5 sono consentiti. Se viene utilizzata la formula di spostamento-pressione, si consiglia un coefficiente di Poisson compreso tra 0,499 e 0,4999.

• I materiali simili alla gomma solitamente si deformano rapidamente con piccoli valori di carico e pertanto richiedono un piccolo carico iniziale.

• Quando vengono utilizzati materiali tipo gomma, a causa del comportamento non lineare del problema, l'aumento rapido del carico risulta spesso in un'instabilità numerica (termini di diagonale negativi nella rigidezza) o nella divergenza durante iterazioni di equilibrio. L'algoritmo di incremento automatico adattivo può essere utile in alcuni casi.

• Il controllo della lunghezza arco o dello spostamento può dimostrarsi più efficiente del controllo della forza quando i termini di diagonale negativi si verificano rapidamente con vari coefficienti di carico.

• Per gli elementi shell con formulazione spessa, l'analisi è semplificata poiché l'incomprimibilità è limitata. La formulazione si basa sul presupposto dell'incomprimibilità perfetta (coefficiente di Poisson pari a 0,5), quindi NUXY viene omesso.

• Le costanti A e B devono essere definite in modo che il risultato sia (A+B) > 0. Per ulteriori informazioni su come determinare i valori delle costanti A e B, fare riferimento a Kao and Razgunas.

Per definire modelli iperelastici...