Crie uma curva definindo a equação para ela.
Quando você cria curvas acionadas por equação, os valores precisam estar em radianos.
Não é possível usar variáveis globais diretamente para curvar acionadas por equação. Contudo, você pode criar uma variável global e associá-la a uma dimensão, depois usar a dimensão na equação para a curva.
Informações adicionais:
- Para controlar a rotação da curva você pode arrastá-la, adicionar relações, etc. A curva atua como qualquer outra curva rígida ou bloco.
- Para aplicar uma escala à curva você precisa considerar a escala na equação. Por exemplo, no exemplo abaixo você pode multiplicar X e Y por 10.
- Para definir as coordenadas inicial e final, para curvas paramétricas, os pontos inicial e final são inicialmente os valores calculado para X e Y em T1 e T2. Você pode transformar a curva adicionando relações ou dimensionando os pontos inicial e final para outros esboços ou à geometria do modelo.
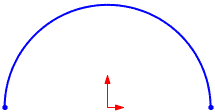
Exemplo de equação explícita:
- yx = sqrt( 4 - x ^ 2)
- x1 = -2
- x2 = 2
|
 |
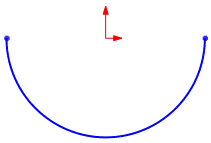
Exemplo de equação paramétrica:
- xt = 50*cos(t)
- yt = 50*sen(t)
- t1 = 0
- t2 = pi
|
 |
Exemplo de curva 3D orientada por equação:
- xt = 2*sin(t)
- yt = 2*cos(t)
- zt = t
- t1 = 0
- t2 = 30
|
 |