Nitinol Material Model
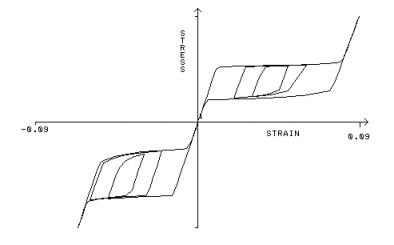
Shape-memory-alloys (SMA) such as Nitinol present the superelastic effect. The term superelastic is used to describe materials with the ability to undergo large deformations in loading-unloading cycles without showing permanent deformations. In fact, under loading-unloading cycles, even up to 10-15% strains, the material shows a hysteretic response, a stiff-soft-stiff path for both loading and unloading, and no permanent deformation.
The Nitinol material model is available for solid and shell elements.
|
|
|
A typical stress-strain response for a Nitinol bar under uniaxial loading conditions. Note that the material behaves differently in tension and compression
|
The stress-strain curve of shape-memory-alloys demonstrate a distinctive macroscopic behavior, not present in traditional materials. This behavior is attributed to the underlying macro-mechanics.
SMA present reversible martensitic phase transformations, that is, a solid-solid diffusion-less transformations between a crystallographically more-ordered phase, “austenite”, and a crystallographically less-ordered phase, “martensite”.
The soft portions of the response curve represent the areas where a phase transformation: a conversion of austenite into martensite (loading), and martensite into austenite (unloading) occurs.
For the sake of simplicity, however, we will refer to the soft behavior on the response curve as “plastic”, and to the stiff portions as “elastic”.
According to this definition, the material first behaves elastically until a certain stress level is reached (the initial yield stress in loading). If the loading continues, the material shows an elastoplastic behavior until the plastic strain reaches its ultimate value. From this point onward, the material behaves elastically again under increased loads.
For unloading, again the material always starts to unload elastically until the stress is reduced to the initial yield stress in unloading. The material will then unload in an elastoplastic manner until all the accumulated plastic strain (from the loading phase) is lost. And from that point onward, the material will unload elastically until it returns to its original shape (no permanent deformation) and zero stress under zero loads.
The Nitinol Model Formulation
Since Nitinol is usually used for its ability to undergo finite strains, the large strain theory utilizing logarithmic strains along with the updated Lagrangian formulation is employed for this model.
The constitutive model is, thus, constructed to relate the logarithmic strains and the Kirchhoff stress components. However, ultimately the constitutive matrix and the stress vector are both transformed to present the Cauchy (true) stresses.
s
s
t1
, s
f
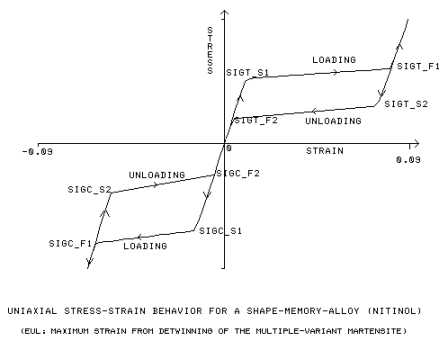
t1 = Initial and Final yield stress for tensile loading. [SIGT_S1, SIGT_F1]
s
s
t2
, s
f
t2 = Initial and Final yield stress for tensile unloading. [SIGT_S2, SIGT_F2]
s
s
c
1
, s
f
c
1 = Initial and Final yield stress for compressive loading. [SIGC_S1, SIGC_F1]
s
s
c2
, s
f
c2 = Initial and Final yield stress for compressive unloading. [SIGC_S2, SIGC_F2]
eul = (Maximum Tensile Plastic Strain)(3/2)0.5
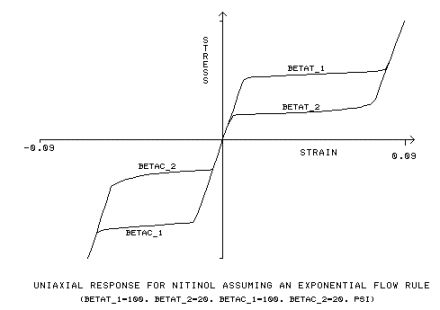
The exponential flow rule, utilizes additional input constants, b
t1, b
t2, b
c1, b
c2:
bt1 = material parameter, measuring the speed of transformation for tensile loading, [BETAT_1]
bt2 = material parameter, measuring the speed of transformation for tensile unloading, [BETAT_2]
bc1 = material parameter, measuring the speed of transformation for compressive loading, [BETAC_1]
bc2 = material parameter, measuring the speed of transformation for compressive unloading, [BETAC_2]
The Yield Criterion
To model the possibility of pressure-dependency of the phase-transformation, a Drucker-Prager-type loading function is used for the yield criterion:
F(
t
) = sqrt(2) s + 3 a p
F- Rif = 0
Where:
s = effective stress
p = mean stress (or hydrostatic pressure)
a = sqrt(2/3) ( s
s
c
1
- s
s
t1
) / ( s
s
c
1 + s
s
t1
)
R
f
i = [ s
f
i ( sqrt (2/3) + a )] : i = 1: loading, i = 2: unloading
The Flow Rule
Through adoption of the logarithmic strain definition, the deviatoric and volumetric components of the strain and stress tensors and their relations can be correctly expressed in a decoupled form.
First, we consider the total plastic & elastic strain vectors to be presented by:
e
p = e
ul x
s ( n + a m )
e
e = e
- e
p
As a result, the Kirchhoff stress vector can be evaluated from:
t = p m + t
p = K ( q - 3 a e
ul x
s
)
t = 2G ( e - e
ul x
s n)
In the above formulations:
eul = scalar parameter representing the maximum material plastic strain deformation [EUL]
xs = parameter between zero & one, as a measure of the plastic straining
q = volumetric strain = e
11 + e
22 + e
33
e = deviatoric strain vector
t = deviatoric stress vector
n = norm of the deviatoric stress: t
/(
sqrt(2) s
)
m = the identity matrix in vector form: {1,1,1,0,0,0}T
K & G = the bulk & Shear elastic moduli: { K = E/[3(1-2n), G = E/[2(1+v)]}
The linear flow rule in the incremental form can be expressed, accordingly:
Loading: Dx
s = ( 1.0 - x
s
) D
F / ( F - R
1
f
)
Unloading: Dx
s = x
s D
F / ( F - R
2
f
)
And the exponential flow rule, used when a nonzero b is defined:
Loading: Dx
s = b
1 ( 1.0 - x
s
) D
F / ( F - R
1
f
)
2
Unloading: Dx
s = b
2 x
s D
F / ( F - R
2
f
)
2
Notes:
• In general, shape-memory-alloys are found to be insensitive to rate-effects. Thus, in the above formulation “time” represents a pseudo variable, and its length does not affect the solution.
• All the equations are presented here for tensile loading-unloading, since similar expressions (with compressive property parameters) can be used for the compressive loading-unloading conditions.
• The incremental solution algorithm here uses a return-map procedure in the evaluation of stresses and constitutive equations for a solution step. Accordingly, the solution consists of two parts. Initially, a trial state is computed; then if the trial state violates the flow criterion, an adjustment is made to return the stresses to the flow surface.
References:
1. Auricchio, F., “A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model,” International Journal of Plasticity, vol. 17, pp. 971-990, 2001.
2. Auricchio, F., Taylor, R.L., and Lubliner, J., “Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior,” Computer Methods in Applied Mechanics and Engineering, vol. 146, pp. 281-312, 1997.
3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. “On Large Strain Elasto-Plastic and Creep Analysis,” Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.
4. Hughes, T., eds. “Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity,” Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.