应力误差

在计算出所有节点处的位移之后，程序继续为每个要素分别计算应变，然后计算应力。在每个要素中的某些点处计算应力。这些点在战略上位于要素内以提供准确结果。称之为高斯点或积分点。

在计算高斯点的应力之后，程序通过外推法计算每个要素的节应力。

如果要获得准确解，所有要素都应该在其公共节处给出完全相同的应力值。尽管通过 FEA 所获得的位移场是连续的，但应力场通常在不同要素中是不连续的。不同要素在公共节处给出一般来说不同的应力值。程序通过对起作用的要素所给出的值求平均值来计算公共节处的节应力。

公共节处的应力变化提供了根据应变能原理测量解的精度的方法。软件按以下方法估计误差分布：

假设：

si*= 相关单元的公共节处的应力

s = 公共节处的平均应力

从公共节处的要素计算出的应力值与平均应力值之间的差值表示为：

从下式计算出每个要素的能量范数中的误差：

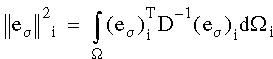
其中 D 为弹性矩阵，Wi 为单元区域。通过求所有要素的误差总和来计算整体误差估计：

其中 n 是要素总数。从下式计算每个要素的百分比误差：

其中 ||u|| 是从下式计算出的总应变能的两倍：

其中 e 是应变向量。

当您设定结果类型为单元数值并设定分量为 ERR: 应力能（在 应力图解 PropertyManager 中）时，标绘出量 h i。请注意，标绘的误差图解是能量范数中的误差估计，而不是应力中的误差。但是，可以看成是代表均匀网格中应力误差的相对分布。p-适应性方法使用此量来改进具有较高能量误差的位置上的结果。

有关误差估计的更多信息，请参阅 International Journal for Numerical Methods in Engineering, vol. 24, 337-357 (1987) 揂 Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis（实用工程分析的简单误差估计法和适用步骤）?，作者 O.C. Zienkiewicz 和 J. Z. Zhu。