Model plastyczny wg Misesa

Kryterium ustępowania można zapisać w postaci:

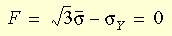
gdzie s jest naprężeniem skutecznym, a s Y jest granicą plastyczności uzyskaną z badań jednoosiowych. Model von Misesa można wykorzystać do opisania zachowania metali. Podczas stosowania tego modelu materiału, należy pamiętać o poniższych zagadnieniach:

• Założono niewielką plastyczność odkształceń w przypadku użycia małych przemieszczeń lub dużych przemieszczeń.

• Przyjęto skojarzone założenie reguły płynięcia.

• Dostępne są zarówno reguły utwardzania izotropowego, jak i kinematycznego. Gdy zarówno promień, jak i środek powierzchni ustępowania w przestrzeni dewiatoryjnej może zmieniać się względem historii obciążenia, wykorzystywana jest liniowa kombinacja utwardzania izotropowego i kinematycznego.

Parametr RK definiuje proporcję utwardzania kinematycznego i izotropowego.

W przypadku czysto izotropowego utwardzania, parametr RK ma wartość 0. Promień powierzchni ustępowania zwiększa się, lecz jej środek pozostaje nieruchomy w przestrzeni dewiatoryjnej.

W przypadku czysto kinematycznego utwardzania, parametr RK ma wartość 1. Promień powierzchni ustępowania pozostaje stały, lecz jej środek może przemieszczać się w przestrzeni dewiatoryjnej.

• Dwuliniowa lub wieloliniowa krzywa jednoosiowego rozciągania może zostać wprowadzona. W przypadku definiowania dwuliniowej krzywej rozciągania, granica plastyczności i współczynnik sprężystości wzdłużnej są wprowadzane za pomocą okna dialogowego Materiał. W przypadku definiowania wieloliniowej krzywej rozciągania, należy zdefiniować krzywą rozciągania.

• Podczas definiowania krzywej rozciągania, pierwszym punktem na krzywej powinien być punkt ustępowania materiału. Właściwości materiału, takie jak współczynnik sprężystości wzdłużnej, granica plastyczności, itp. zostaną pobrane z krzywej rozciągania, jeżeli jest dostępna, a nie z tabeli właściwości materiału w oknie dialogowym Materiał. Tylko współczynnik Poissona (NUXY) zostanie pobrany z tabeli.

Definiowanie krzywych rozciągania nie jest obsługiwane w badaniach testu upuszczenia.

• Parametry granicy plastyczności i współczynnika sprężystości dla dwuliniowej krzywej rozciągania można skojarzyć z krzywymi temperaturowymi, aby wykonać analizę termoplastyczną.

• Zalecane jest użycie metody iteracyjnej NR (Newton-Raphson).

Model Huber-von Mises może być używany z elementami bryłowymi (jakości roboczej i wysokiej) oraz grubej skorupy (jakości roboczej i wysokiej) .

Termoplastyczność nie jest dostępna dla elementów skorupowych.

Poniższy rysunek przedstawia typową krzywą rozciągania materiału plastycznego:

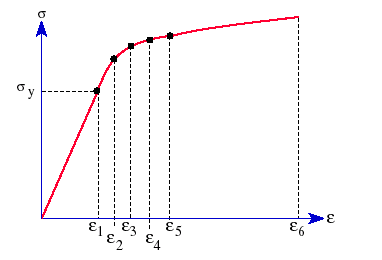
Analiza dużego odkształcenia

W teorii plastyczności dużego odkształcenia definiowana jest logarytmiczna miara odkształcenia jako:

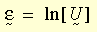
gdzie: U jest właściwym tensorem rozciągnięcia, zwykle uzyskiwanym z właściwego rozkładu biegunowego gradientu deformacji F (tj. F = R U, R jest tensorem obrotu). Przyrostowe odkształcenie logarytmiczne jest obliczane jako:

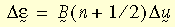
gdzie: B (n+1/2) jest macierzą odkształcenia-przemieszczenia obliczaną w kroku rozwiązania n+1/2, a D u jest przyrostowym wektorem przemieszczeń. Należy zauważyć, że powyższa postać jest przybliżeniem drugiego stopnia dokładnego wzoru.

Natężenie naprężenia przyjęto jako natężenie Greena-Naghdiego, aby uzyskać prawidłową niezmienność lub obiektywność konstytucyjnego modelu. Poprzez transformację natężenia naprężenia z układu globalnego do układu R,

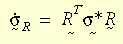
Cały model konstytucyjny przybierze identyczną postać jak w teorii małego odkształcenia. Teoria plastyczności dużego odkształcenia jest stosowana do kryterium ustępowania von Misesa, skojarzonej reguły płynięcia oraz izotropowego lub kinematycznego utwardzania (dwuliniowego lub wieloliniowego). Zależność właściwości materiału od temperatury materiału jest obsługiwana przez dwuliniowe utwardzanie. W bieżącym przypadku używany jest algorytm promieniowo-powrotny. Podstawową zasadą jest przybliżenie wektora normalnego N przez:

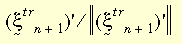
gdzie:

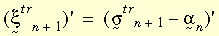
Poniższy rysunek ilustruje powyższe dwa równania.

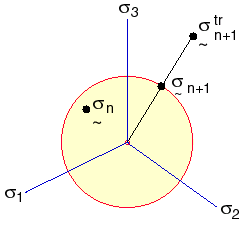
Wektor siły elementu i macierze sztywności są obliczane w oparciu o zaktualizowane wyrażenie Lagrange'a. Naprężenia Cauchy'ego, naprężenia logarytmiczne i bieżąca grubość (tylko w elementach skorupowych) są zapisywane w pliku wyjściowym.

Sprężystość w bieżącym przypadku jest modelowana w postaci hipersprężystej, która zakłada niewielkie odkształcenia elastyczne, lecz dopuszcza dowolnie duże odkształcenia plastyczne. W przypadku problemów sprężystych dużego odkształcenia można użyć hipersprężystych modeli materiału, takich jak Mooney-Rivlin.

Naprężenie Cauchy'ego (rzeczywiste) i naprężenie logarytmiczne należy użyć przy definiowaniu wieloliniowej krzywej rozciągania.

Porównanie kryteriów plastyczności wg Tresca i von Misesa