Modelo de plasticidade - von Mises
O critério de resistência pode ser escrito desta forma:
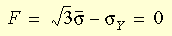
onde s é a tensão eficaz e s
Y é o limite de resistência dos testes uniaxiais. O modelo de von Mises pode ser usado para descrever o comportamento de metais. Devem ser observadas as considerações a seguir quando este modelo de materiais for usado:
-
É assumida uma plasticidade de pequena deformação quando são usados pequenos ou grandes deslocamentos.
-
É feita uma pressuposição de regra de fluxo associada.
-
As regras de endurecimento isótropico e cinemático estão disponíveis. Uma combinação linear de endurecimento isotrópico e cinemático é implementada quando tanto o raio como o centro da superfície de escoamento no espaço desviatório podem variar com relação ao histórico de carregamento.
O parâmetro RK define a proporção de endurecimento cinemático e isotrópico.
Para o endurecimento isotrópico puro, o parâmetro RK tem o valor 0. O raio da superfície de escoamento se expande mas seu centro permanece fixo no espaço desviatório.
Para o endurecimento cinemático puro, o parâmetro RK tem o valor 1. O raio da superfície de escoamento se permanece constante enquanto seu centro pode se mover no espaço desviatório.
-
Pode ser inserida uma curva de tensão-deformação uniaxial bilinear
ou multilinear para a plasticidade. Para a definição da curva de tensão-deformação bilinear, os módulos de limite de resistência e elástico são inseridos pela caixa de diálogo
Material
. Para a definição da curva de tensão-deformação multilinear deve ser definida uma curva de tensão-deformação.
-
Quando uma curva de tensão-deformação é definida, o primeiro ponto na curva deve ser o ponto de escoamento do material. As propriedades do material, como o módulo elástico, o limite de escoamento etc. serão obtidas na curva tensão-deformação, quando disponível, e não da tabela de propriedades do material da caixa de diálogo Material . Somente o coeficiente de Poisson (NUXY) será obtido da tabela.
 A definição de curvas de tensão-deformação não tem suporte para estudos de teste de queda.
A definição de curvas de tensão-deformação não tem suporte para estudos de teste de queda.
-
Os parâmetros de limite de escoamento e módulo elástico para descrição da curva de tensão-deformação bilinear podem ser associados a curvas de temperatura para a execução de análises termoplásticas.
-
É recomendável usar o método iterativo de NR (Newton-Raphson).
O modelo Huber-von Mises pode ser usado com sólidos (qualidades rascunho e alta) e com elementos de cascas espessas (qualidades rascunho e alta) .
 A termoplasticidade não está disponível para elementos de casca.
A termoplasticidade não está disponível para elementos de casca.
A figura a seguir mostra uma curva de tensão-deformação típica de material plástico.
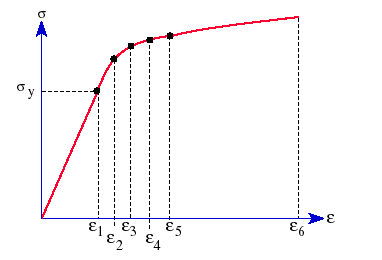
Análise de grandes deformações
Na teoria de plasticidade para grandes deformações, uma medida logarítmica da deformação é definida como:
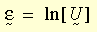
onde U é o tensor de alongamento direito, geralmente obtido pela decomposição polar à direita do gradiente de deformação F (i.e., F = R U, R é o tensor de rotação). A deformação logarítmica incremental é estimada como:
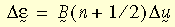
onde B
(n+1/2) é a matriz de deformação-deslocamento estimada na etapa de solução n+1/2 e D
u é o vetor dos deslocamentos incrementais. Observe que a forma acima é uma aproximação de segunda ordem da fórmula exata.
A taxa de tensão é obtida como a taxa Green-Naghdi, de modo a fazer com que o modelo constitutivo seja adequadamente independente de quadro ou objetivo. Pela transformação da taxa de tensão do sistema global para o sistema R:
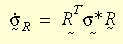
O modelo constitutivo inteiro terá forma idêntica à da teoria de pequena deformação. A teoria de plasticidade para grandes deformações é aplicada ao critério de escoamento de von Mises, à lei do fluxo associativo e ao endurecimento isotrópico ou cinemático (bilinear ou multilinear). A dependência da temperatura da propriedade do material é suportada pelo endurecimento bilinear. O algoritmo de retorno radial é usado no caso atual. A ideia básica é fazer uma aproximação do vetor normal N por:
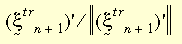
onde:
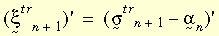
A figura a seguir ilustra as duas equações acima.
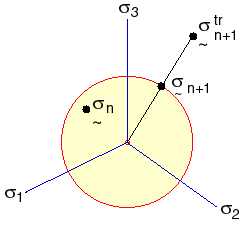
O elemento vetor de força e as matrizes de rigidez são calculados com base na fórmula de Lagrange atualizada. As tensões de Cauchy, as tensões logarítmicas e a espessura atual (somente elementos casca) estão gravadas no arquivo de saída.
A elasticidade no caso atual é modelada na forma hiperelástica que pressupõe pequenas deformações elásticas, mas aceita deformações plásticas arbitrariamente grandes. Para problemas de elasticidade de grandes deformações (do tipo borracha), você pode usar modelos de materiais hiperelásticos, como o de Mooney-Rivlin.
 As tensões de Cauchy (verdadeiras) e as deformações logarítmicas podem ser usadas na definição da curva tensão-deformação multilinear.
As tensões de Cauchy (verdadeiras) e as deformações logarítmicas podem ser usadas na definição da curva tensão-deformação multilinear.
Comparação entre os critérios de Tresca e von Mises para plasticidade