Einfreiheitsgradsysteme (SDOF-Systeme)
Betrachten Sie das einfache Massefedersystem. Die Masse (m) wird einer Kraft F(t) in Richtung u als Funktion der Zeit ausgesetzt. Die Masse kann sich nur in Richtung u bewegen. Daher handelt es sich hier um ein Einfreiheitsgradsystem (SDOF). Der Bewegung wird durch eine Feder der Steifigkeit (k) Widerstand geleistet.
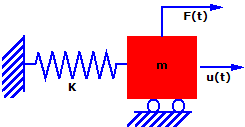
Wenn für dieses System zum Zeitpunkt (t) das zweite Newtonsche Gesetz (Kraft = Masse mal Beschleunigung) angewendet wird, ergibt sich Folgendes:
F(t)-ku(t) = mu..(t)
oder
mu..(t) + ku(t) = F(t)
wobei:
u..(t) ist die Beschleunigung der Masse zum Zeitpunkt (t) und entspricht in Bezug auf die Zeit der zweiten Ableitung von u
k = Steifigkeit der Feder
Theoretisch vibriert die Masse, wenn sie verschoben und losgelassen wird, unendlich mit der gleichen Amplitude. Praktisch vibriert die Masse in immer kleineren Amplituden, bis sie zum Stillstand kommt. Dieses Phänomen wird als Dämpfung bezeichnet, die durch einen Energieverlust aufgrund von Reibung und anderen Effekten verursacht wird. Dämpfung ist ein komplexes Phänomen. Hier wird von der Annahme ausgegangen, dass die Dämpfungskraft proportional zur Geschwindigkeit ist. Dieser Dämpfungstyp wird als viskose Dämpfung bezeichnet.
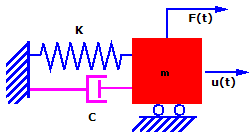
Unter Berücksichtigung der Dämpfung lautet die obige Gleichung wie folgt:
mu..(t) + cu.(t) + ku(t) = F(t)
wobei:
u..(t) ist die Beschleunigung der Masse zum Zeitpunkt (t) und entspricht in Bezug auf die Zeit der ersten Ableitung von u
In statischen Studien sind Geschwindigkeit und Beschleunigung so gering, dass sie vernachlässigbar sind, und F und u sind keine Funktionen der Zeit. Die obige Gleichung reduziert sich auf F=ku.
Mehrfreiheitsgradsysteme (MDOF-Systeme)
Bei einem Mehrfreiheitsgradsystem (MDOF) werden m, c und k zu Matrizen (anstelle von Einzelwerten). Die Bewegungsgleichungen werden wie folgt ausgedrückt:
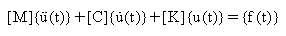
wobei:
[M]: Massenmatrix
[K] : Steifigkeits-Matrix
[C] : Dämpfungsmatrix
{u(t)}: Verschiebungsvektor zum Zeitpunkt t (Verschiebungskomponenten der einzelnen Knoten)
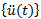 : Beschleunigungsvektor zum Zeitpunkt t (Beschleunigungskomponenten der einzelnen Knoten)
: Beschleunigungsvektor zum Zeitpunkt t (Beschleunigungskomponenten der einzelnen Knoten)
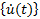 : Geschwindigkeitsvektor zum Zeitpunkt t (Geschwindigkeitskomponenten der einzelnen Knoten)
: Geschwindigkeitsvektor zum Zeitpunkt t (Geschwindigkeitskomponenten der einzelnen Knoten)
{f(t)}: zeitabhängiger Lastvektor (Kraftkomponenten der einzelnen Knoten)