Hyperelastisches Ogden-Modell

Die Ogden-Dehnungsenergiedichte-Funktion wird definiert als:

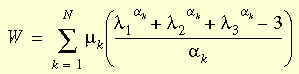
wobei: λ_i die Hauptdehnungen sind, α_i, μ_i Materialkonstanten sind und N die Anzahl der Ausdrücke in der Funktion ist. Diese Funktion wird als eine der hilfreichsten Funktionen zur Beschreibung großer Verformungen bei gummiartigen Materialien angesehen.

Die Pönalenfunktion, die in der Formel des Ogden-Modells verwendet wird, hat die Form der im Mooney-Rivlin-Modell verwendeten. Die verwendete Dehnungsenergie-Funktion ist eine modifizierte Art der Ogden-Funktion:

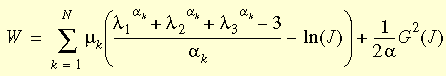
wobei J das Verhältnis des Verformungsvolumens zum nicht verformten Volumen ist, N die Anzahl der Ausdrücke in der Funktion ist, G(J) = J²-1 und Folgendes gilt:

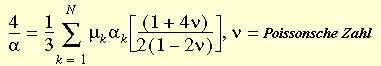
Modelle mit 3 Ausdrücken (Ogden modifiziert) sind weit verbreitet. Im Programm sind Modelle mit bis zu 4 Ausdrücken (N = 4) verfügbar.

Neben den oben genannten Materialkonstanten ist auch die Poissonsche Zahl erforderlich. In den meisten Fällen werden zufrieden stellende Ergebnisse mit einer Poissonschen Zahl zwischen 0.49 und 0.499 erzielt. Wenn die Poissonsche Zahl weiter erhöht wird, hat dies keinen merklichen Einfluss auf die numerischen Ergebnisse, es sei denn, es liegt beachtliche volumetrische Dehnung vor.

Wenn die Poissonsche Zahl ganz nahe an 0,5 herankommt, kann die Lösung abgebrochen werden, weil in der Steifigkeitsmatrix negative diagonale Ausdrücke auftreten oder keine Konvergenz vorhanden ist.