Когда к телу прикладываются нагрузки, оно пытается компенсировать их воздействие, создавая внутренние силы, которые в целом изменяются от одной точки к другой. Интенсивность этих внутренних сил называется напряжением. Единицы напряжения: сила на площадь сегмента.
Компоненты напряжения
Представим, что на балку действуют силы сжатия. Состояние напряжения в точке P можно описать в показателях произвольной плоскости. Несмотря на то что результирующее напряжение во всех случаях является одинаковым, значения компонентов напряжения зависят от выбранной плоскости.
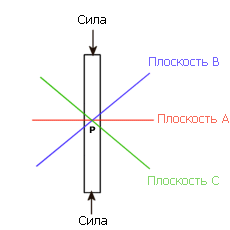
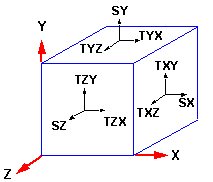
Напряжение описывается величиной, направлением и плоскостью, на которую оно действует. Состояние напряжения в какой-то точке полностью описывается следующими компонентами:
|
SX |
Напряжение в направлении X, действующее перпендикулярно плоскости YZ |
|
SY |
Напряжение в направлении Y, действующее перпендикулярно плоскости XZ |
|
SZ |
Напряжение в направлении Z, действующее перпендикулярно плоскости XY |
|
TXY |
Напряжение в направлении Y, действующее на плоскость, перпендикулярную направлению X (плоскость YZ) |
|
TYX |
Напряжение в направлении X, действующее на плоскость, перпендикулярную направлению Y (плоскость XZ) |
|
TXZ |
Напряжение в направлении Z, действующее на плоскость, перпендикулярную направлению X (плоскость YZ) |
|
TZX |
Напряжение в направлении X, действующее на плоскость, перпендикулярную направлению Z (плоскость XY) |
|
TYZ |
Напряжение в направлении Z, действующее на плоскость, перпендикулярную направлению Y (плоскость XZ) |
|
TZY |
Напряжение в направлении Y, действующее на плоскость, перпендикулярную направлению Z (плоскость XY)
|
SX, SY и SZ называются нормальными напряжениями. TXY, ...., TZY называются касательными напряжениями. Касательные напряжения удовлетворяют следующим уравнениям: TXY = TYX, TXZ = TZX, и TYZ = TZY. Таким образом, состояние напряжения в какой-то точке полностью определяется шестью компонентами:
Главные напряжения
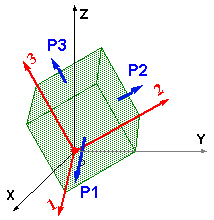
Для каждой точки существует плоскость, для которой отсутствуют касательные напряжения. Состояние напряжений относительно этой плоскости полностью определяется нормальными напряжениями.
|
P1 |
Нормальное напряжение в первом главном направлении (самое большое). |
|
P2 |
Нормальное напряжение во втором главном направлении (промежуточное). |
|
P3 |
Нормальное напряжение в третьем главном направлении (самое малое). |
|
|
Эквивалентное напряжение (также называется напряжением von Mises)
В SimulationXpress можно осмотреть величину напряжения, которая называется эквивалентным (или von Mises) напряжением. Несмотря на то, что эквивалентное напряжение в какой-то точке не однозначно определяет состояние напряжения в этой точке, оно предоставляет достаточную информацию, чтобы оценить надежность конструкции для многих пластичных материалов.
В отличие от компонентов напряжения эквивалентное напряжение не имеет направления. Оно полностью определяется величиной, выраженной в единицах напряжения. Чтобы рассчитать коэффициенты запаса прочности в различных точках, SimulationXpress использует Критерий текучести von Mises, который точно определяет то, что материал начинает переходить в состояние текучести в какой-то точке, когда эквивалентное напряжение достигает предела текучести материала.