Система уравнений движения линейной системы с n степенями свободы, возбужденной изменяющейся во времени силой:
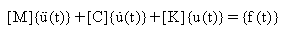(Уравнение 1).
где:
[М] = n x n симметричная матрица инерции
[C] = n x n симметричная матрица демпфирования
[К] = n x n симметричная матрицы жесткости
{f(t)} = n-мерный вектор силы
, 
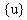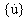и 
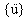являются n-мерными векторами перемещения, скорости и ускорения, соответственно.
(Уравнение 1) является системой n обычных совместных дифференциальных уравнений с постоянными коэффициентами. Уравнения движения связаны через условия массы, жесткости и демпфирования. Связь зависит от системы координат, используемой для описания уравнения движения математически.
Основной идеей модального анализа (исследование методом разложения по собственным формам колебаний) является преобразование связанной системы (Уравнения 1) в ряд независимых уравнений, используя модальную матрицу [F] в качестве матрицы преобразования. [Φ] содержит нормальные моды {f}i для i = 1,....,n, расположенные следующим образом:
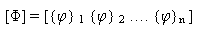(Уравнение 2).
Нормальные моды и собственные значения системы получаются из решения задачи о собственных значениях:
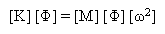(Уравнение 3).
где [ω2] является диагональной матрицей собственных частот в квадрате.
Для линейных систем, система n уравнений движения может разделяться на n уравнений с одной степенью свободы в исчислении модального вектора перемещения {x:}:
(Уравнение 4).
Подставив вектор {u} из (Ур. 4) и умножив его на [Φ]T (Уравнение 1), получим:
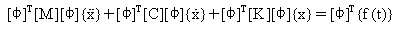(Уравнение 5).
Нормальные моды удовлетворяют свойству ортогональности, а модальная матрица [Φ] является нормализованной, чтобы удовлетворять следующим уравнениям:
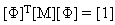(Уравнение 6).
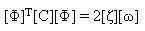(Уравнение 7) и
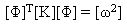(Уравнение 8).
Посредством подстановки (Уравнений 6-8), (Уравнение 5) становится системой n независимых дифференциальных уравнений второго порядка (SDOF):
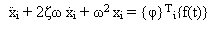для i =1,..., n (Уравнение 9)
(Уравнение 9) решено, используя пошаговые методы интегрирования, такие как Wilson-Theta и Newmark.
Интегрирование выполняется во временной области, где использованы результаты последнего шага для прогнозирования следующего шага.
Вектор перемещения системы (u) получается из (Уравнения 4).