Model nieliniowy sprężysty

Typowa krzywa rozciągania modelu nieliniowego materiału to:

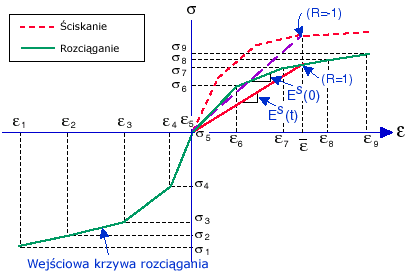
W szczególnym przypadku historii naprężeń związanej z obciążaniem proporcjonalnym, gdzie komponenty tensora naprężenia zmieniają się monotonicznie w stałym stosunku do siebie nawzajem, odkształcenia można wyrazić w funkcji końcowego stanu naprężenia w następującej postaci:

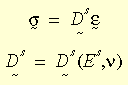
D^s jest sieczną macierzą materiału, E^s jest modułem siecznym, a ν jest współczynnikiem Poissona

Aby wykorzystać ten model, należy zdefiniować współczynnik Poissona oraz krzywą rozciągania materiału.

Całkowity wektor odkształcenia ε jest używany do obliczenia skutecznego naprężenia ε, co pozwala uzyskać moduł sieczny ze zdefiniowanej przez użytkownika krzywej materiałowej (rozciągania). W przypadku stosowania trzech wymiarów:

Krzywa rozciągania od trzeciego kwadrantu (ściskanie) do pierwszego kwadrantu (rozciąganie) ma zastosowanie do tego modelu dla elementów dwuwymiarowych i trójwymiarowych z pewnymi modyfikacjami. Aby uzyskać styczne i sieczne moduły materiałowe wykorzystywana jest metoda interpolacji. Definiowanie proporcji R, która jest funkcją odkształcenia wolumetrycznego Φ, odkształcenia skutecznego i współczynnika Poissona R, przybiera następującą postać:

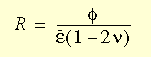
Zauważono, że R = 1 przedstawia przypadek rozciągania jednoosiowego, a R = -1 przedstawia przypadek ściskania. Te dwa przypadki określają górną i dolną granicę, w taki sposób, że gdy R przekracza te dwie wartości, program wymusza wartość graniczną. Model nieliniowy sprężysty materiału może być używany z siatkami bryłowymi i skorupowymi.