本體中各點的內部力都不同。對於任何小面積的內部平面,負載是由本體的一側施加在另一側上。應力代表這些內部力的強度 (每單位面積上的力)。
應力
在連續體中,您可依照下列方式計算點的應力:
- 想像有一個切過本體上該點的任意平面,
- 而在平面上該點附近有一個無限小的面積 ΔA,
- 假設以特定方向傳至 ΔA 的力值為 ΔF,
- ΔA 趨近於 0 時該方向上的應力為 ΔF/ΔA。
上述說明在於定義某一點的應力或拖曳力向量。而拖曳力向量並非純粹定義某一點的應力狀態。其值會隨著所選的任意平面而改變。應力張量舉例來說,實際應力張量定義為 σ = n.T (矩陣乘法),其中 n 是與平面相關的法向向量,而 T 則是專門定義應力的應力或拖曳力向量。
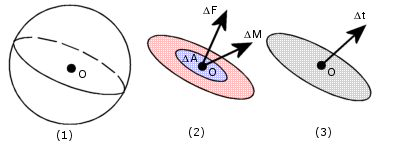
圖 (1):通過 O 點的平面將本體分為兩部分。
圖 (2):在平面上 ΔA 區域 O 點附近的合成力及力矩向量。
圖 (3):限制平面上 O 點的應力向量。
應變
應變為 δ 長度變化量與原始長度 L 的比值。應變為無因次的量值。
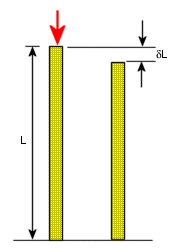
應變 = δL/L
計算順序
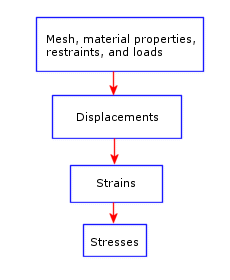
假設一網格化模型有一組位移拘束及負載,線性靜態分析程式會進行如下:
- 程式會建構並對線性聯立有限元素平衡方程式系統求解,以計算每個節點的位移組成。
- 然後程式會使用位移結果來計算應變組成。
- 程式會使用應變結果及應力 - 應變關係來計算應力。
應力計算
程式會先計算特殊點的應力結果,這些點稱為高斯點或求積點,位於每個元素內部。程式會選擇這些點以產生最佳的數值結果。然後,程式會外推高斯點的可用結果,以計算每個元素的節點應力。
在成功執行後,資料庫中就可取得每個元素的節點應力結果。兩或多個元素共用的節點會得出不同的結果。一般而言,這些結果之所以不一致是因為有限元素方法是一種近似值方法。例如,如果 3 個元素共用某一節點,則該節點的每個應力零組件可能會有 3 個略有差異的值。
當檢視應力結果時,您可要求元素應力或節點應力。若要計算元素應力,程式會將每個元素的對應節點應力加以平均。若要計算節點應力,程式會將共用該節點的所有元素之對應結果加以平均。