L'analyse harmonique évalue la réponse maximale d'un système en régime permanent à des chargements harmoniques.
A chaque pas de simulation, tous les chargements appliqués et toutes les excitations de base ont la même fréquence. Ces intensités sont définies par les courbes en fréquence associées.
Supposons un vecteur de force nodale harmonique (P) défini de la façon suivante:
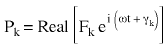(Equation 1) ou 
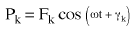(Equation 2),
où :
Pk est l'intensité de la force dans la direction du kième degré de liberté
ω est la fréquence d'excitation et
γk est l'angle de phase de la force.
Dans le cas des systèmes linéaires, les équations de mouvement sont découplées en n équations modales:
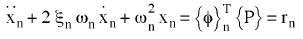(Equation 3).
La substitution du vecteur de force {P} dans (Equation 3) donne les résultats suivants:
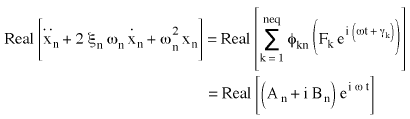(Equation 4), où
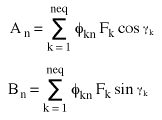(Equation 5)
La solution en régime permanent de (Equation 4) est:
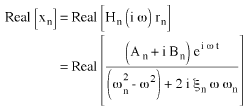(Equation 6).
La partie réelle de (Equation 6) est:
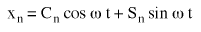(Equation 7), où
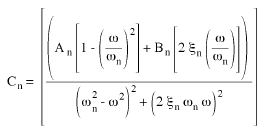(Equation 8) et
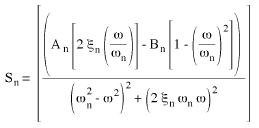(Equation 9).
Le vecteur de déplacement u est donné par :
(Equation 10) ou
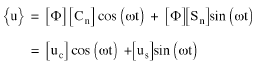(Equation 11)
L'amplitude du déplacement uk et l'angle de phase correspondant θk pour le kième degré de liberté sont :
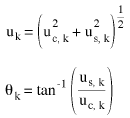(Equation 12)
Les réponses de vitesse et d'accélération découlent des dérivées de (Equation 11). Leurs amplitudes sont:
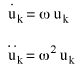(Equation 13)
Les angles de phase des vitesses et des accélérations sont déphasées de 90º et 180º par rapport aux angles de phase de déplacement.