Eine harmonische Analyse bewertet eine stationäre Spitzenreaktion eines Systems auf harmonische Lasten.
Bei allen Lösungsschritten haben alle angewendeten Lasten und Basiserregungen dieselbe Frequenz. Die Magnituden werden durch die assoziierten Frequenzkurven definiert.
Nehmen wir einen harmonischen Knotenkraftvektor {P} an, definiert als:
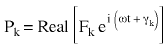 (Gleichung 1) oder
(Gleichung 1) oder 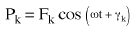 (Gleichung 2),
(Gleichung 2),
wobei:
Pk die Magnitude der Kraft in die Richtung des kten Freiheitsgrads ist
ω die Erregungsfrequenz ist und
γk der Phasenwinkel der Kraft ist.
Bei linearen Systemen werden die Systemgleichungen für Bewegung in n Schwingungsgleichungen abgekoppelt:
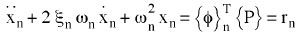 (Gleichung 3).
(Gleichung 3).
Ein Ersetzen des Kraftvektors {P} in (Gleichung 3) führt zu:
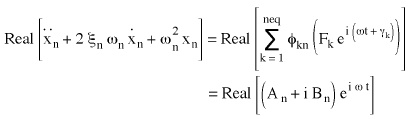 (Gleichung 4), wo
(Gleichung 4), wo
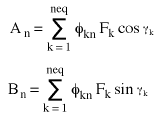 (Gleichung 5)
(Gleichung 5)
Die stationäre Lösung für (Gleichung 4) ist:
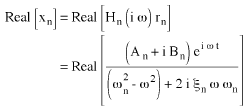 (Gleichung 6).
(Gleichung 6).
Der echte Teil von (Gleichung 6) ist:
 (Gleichung 7) wo
(Gleichung 7) wo
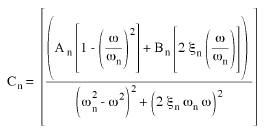 (Gleichung 8) und
(Gleichung 8) und
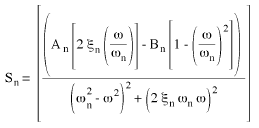 (Gleichung 9).
(Gleichung 9).
Der Verschiebungsvektor u ist gegeben durch:
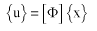 (Gleichung 10) oder
(Gleichung 10) oder
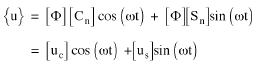 (Gleichung 11)
(Gleichung 11)
Die Magnitude der Verschiebung uk und der entsprechende Phasenwinkel θk für den kten Freiheitsgrad sind:
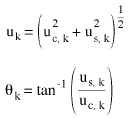 (Gleichung 12)
(Gleichung 12)
Die Geschwindigkeits- und Beschleunigungsreaktionen werden von den Derivaten von (Gleichung 11) abgeleitet. Ihre Amplituden sind:
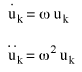 (Gleichung 13)
(Gleichung 13)
Die Phasenwinkel der Geschwindigkeiten und Beschleunigungen sind 90º und 180º außerhalb der Phase hinsichtlich der Verschiebungs-Phasenwinkel.