Opposto a un materiale isotropo, un materiale ortotropo ha direzioni di forza privilegiate tra loro perpendicolari. Le proprietà lungo queste direzioni (note anche come direzioni principali) sono i valori estremi dei coefficienti di elasticità.
La matrice [D] per un materiale ortotropico ha nove proprietà elastiche indipendenti. Inoltre, esistono tre proprietà per l'espansione termica.
Relazioni di sollecitazione-deformazione ortotrope 2D
In 2D, le relazioni di sollecitazione-deformazione ortotrope possono essere scritte nel modo seguente, inclusi gli effetti di temperatura:
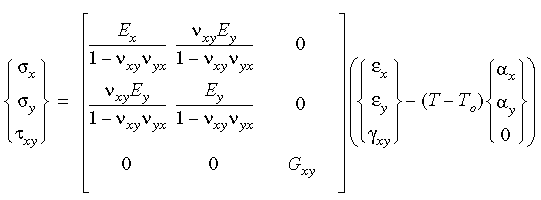
Per soddisfare la simmetria nella matrice dei moduli elastici, νxy Ey = νyx Ex.
è necessario soddisfare la condizione di simmetria precedente quando vengono immessi i valori numerici del modulo elastico o del coefficiente di Poisson.
Inoltre, se non viene specificato il valore numerico del modulo di taglio, verrà calcolato dal software nel modo seguente:
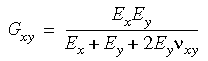
In 3D, le condizioni di simmetria ortotropa impongono:
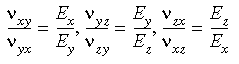
Quando vengono immesse le proprietà del materiale ortotropo in 3D, è necessario accertare che le condizioni di simmetria sopra descritte non siano violate. Si osservi che se non vengono specificati i valori numerici dei moduli di taglio, verranno calcolati dal software utilizzando le relazioni seguenti: 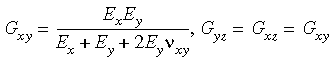
Se Ex = Ey = Ez, il software calcolerà i moduli di taglio internamente anche se definiti esplicitamente. Il software assume un valore di 0,0 per il coefficiente di Poisson non definito esplicitamente.