調和解析を使用して、調和荷重または地盤振動による定常最大応答を計算します。
調和荷重 P は P = A sin (ωt + φ) により数式化されます。ここで、A は振幅、ω は固有値、t は時間、φ は位相角を表します。異なる固有値 w の調和荷重 vs 時間の例を見てみます:
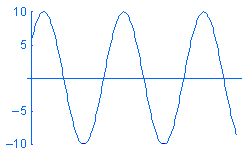
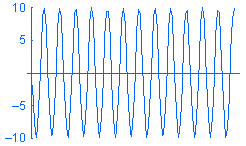
モーダル時刻歴スタディを作成し、時間の関数で荷重を定義することもできますが、時間による応答の過渡変動には興味がない場合もあります。 そのような場合は、調和解析を使用して、目的とする動作周波数域における定常最大応答を解析することで、時間とリソースの節約が行えます。
たとえば、試験テーブルに設置されたモーターの場合、調和荷重をボルトを通して支持システムへ伝達します。この支持システムをモデル化し、調和解析スタディを定義することで、モーターの周波数域における定常最大変位や応力等の評価を行うことが可能になります。モーターは分布質量で近似します。
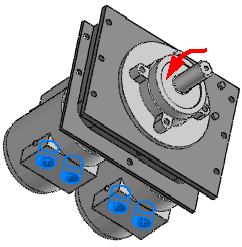
スタディの実行後は、動作固有値幅にわたる最大応力、変位、加速度、速度、および応答の位相角の確認が行えます。
この種類の解析では、モーダル、Rayleigh、および複合モーダルの減衰オプションが使用できます。