응력 싸이클의 교번응력이 싸이클의 응력 영역의 1/2로 계산됩니다. 응력 싸이클로 인한 손상도는 교차 응력뿐만 아니라 평균 응력에 따라 다릅니다. 예를 들어, 아래의 두 싸이클에 같은 교차 응력이 있으나 평균 응력이 다르므로, 손상도가 다릅니다.
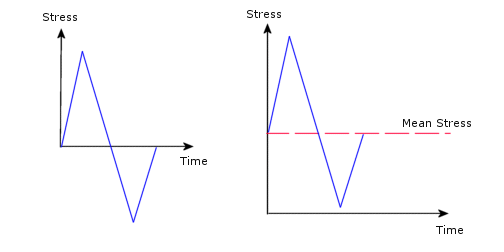
Haigh 도표로 불리우는 다음 도표는 싸이클의 평균 응력이 실패에 주는 영향을 보여줍니다.
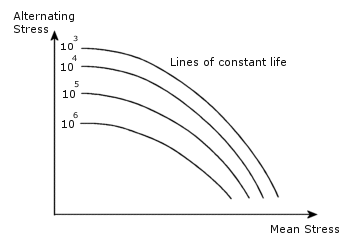
하중이 완전 역방향일 경우에만 평균 응력이 0 입니다. 하중과 같은 R-비가 있는 S-N 곡선이 제공된 경우가 대표적입니다. 이 경우, 수정이 필요없으므로 S-N 곡선이 직접 사용됩니다. 다른 R 비율로 S-N 곡선을 정의하면, 곡선사이의 선형 보간법으로 평균 응력을 고려합니다. 로딩하는 R-비와 다른 비율이 있는 S-N 곡선만이 제공되면, 수정이 필요합니다.
평균 응력 계산에는 항상 von Mises 응력이 사용됩니다. von Mises가 양수의 수량일 때, 연관 평균 응력 계산을 목적으로 첫 평균 주응력의 기호가 그 수량으로 지정됩니다.
정의
수정 방법을 설명하기 위해, 응력 싸이클의 변수를 다음과 같이 정의하겠습니다.
Smax = 최대 응력
Smin = 최소 응력
ΔS = 응력 영역 = Smax - Smin
Sa = 교차 응력 = (Smax - Smin)/2
Smean = 평균 응력 = (Smax + Smin)/2
R = 응력 비율 = Smin/Smean
A = 폭 비율 = Sa/Smean
일부 공통 하중의 응력과 폭 비율이 표시됩니다.
| 하중 유형
|
응력과 폭 비율
|
|---|
| 역방향
|
R = -1, A = 무한
|
| 0 에서 최대값까지
|
R = 0, A = 1
|
| 0 에서 최소값까지
|
R = 무한, A = -1
|
수정 방식
다음과 같이 합니다.
ca = 수정된 교번 응력 (0 평균 기반),
Sy = 항복 응력,
Su = 극한 응력
S
ca 계산을 위해 다음 방식이 제공됩니다.
| 방식
|
수식
|
|---|
| 1. Goodman - 일반적으로 파손되기 쉬운 재질에 적합합니다.
|
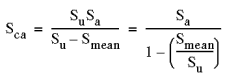 |
| 2. Gerber 방식 - 일반적으로 연성 재질에 적합합니다
|
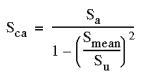 |
| 3. Soderberg 방식 - 일반적으로 가장 무난한 방식입니다
|
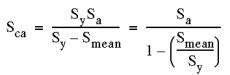 |
부동 폭 이벤트와 유동 폭 이벤트 모두에, 각 싸이클에 대한 교번응력과 더불어 평균응력이 계산된 후 지정한 방법을 통해 수정된 응력이 계산됩니다.