Puesto que Nitinol generalmente se utiliza por su capacidad de soportar deformaciones unitarias finitas, se emplea para este modelo la teoría de la gran deformación unitaria mediante deformaciones unitarias logarítmicas junto con la formulación lagrangiana actualizada.
El modelo constitutivo, por lo tanto, se construye para relacionarse con las deformaciones unitarias logarítmicas y los componentes de tensiones de Kirchhoff. Sin embargo, la matriz constitutiva y el vector de deformación unitaria finalmente se transforman para presentar las tensiones de Cauchy (verdaderas).
|
σst1, σft1
|
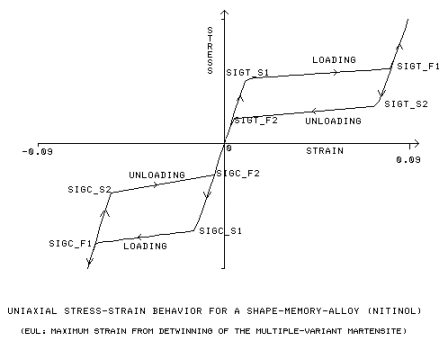
Límite elástico inicial y final para carga de tracción [SIGT_S1, SIGT_F1]
|
|
σst2, σft2
|
Límite elástico inicial y final para descarga de tracción [SIGT_S2, SIGT_F2]
|
|
σsc1, σfc1
|
Límite elástico inicial y final para carga de compresión [SIGC_S1, SIGC_F1]
|
|
σsc2, σfc2
|
Límite elástico inicial y final para descarga de compresión [SIGC_S2, SIGC_F2]
|
|
eul
|
(Deformación unitaria plástica tangencial máxima) *(3/2)0.5
|
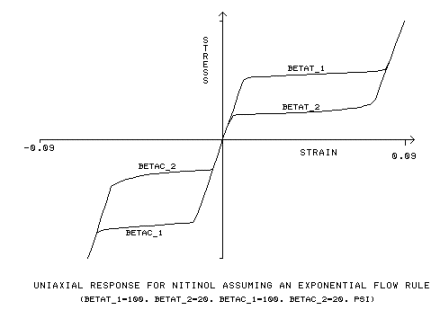
La regla de flujo exponencial utiliza constantes de entrada adicionales, β
t1, β
t2, β
c1, β
c2:
|
βt1
|
parámetro de material que mide la velocidad de transformación para la carga de tracción, [BETAT_1]
|
|
βt2
|
parámetro de material que mide la velocidad de transformación para la descarga de tracción, [BETAT_2]
|
|
βc1
|
parámetro de material que mide la velocidad de transformación para la carga de compresión, [BETAC_1]
|
|
βc2
|
parámetro de material que mide la velocidad de transformación para la descarga de compresión, [BETAC_2]
|
El criterio de flexibilidad
Para modelar la posibilidad de que se produzca una dependencia de la presión por parte de la transformación de fase, se utiliza una función de carga de tipo Drucker-Prager para el criterio de flexibilidad:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RIf = 0
donde
σ(bar) = tensión efectiva
p = tensión media (o presión hidrostática)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 - σst1)
RfI = [ σfI(sqrt(2/3) + α)], I = 1 para carga y 2 para descarga