目前已發展出不同的控制技術來執行非線性分析。這些技術可分為:
增量負載控制方法
在此種策略中,會以套用至系統的負載做為規定的變數。平衡路徑上的每個狀態 (點) 都由一表面 (F = 常數) 與路徑的相交點來決定,以判斷變形參數。
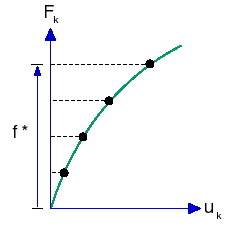
在有限元素分析中使用此種技術,負載 (基本運動、規定的位移、熱、重力等等) 都會依相關「時間」曲線中的指定,以漸增方式套用。
增量位移控制方法
使用此技術時,平衡路徑上的一點是由固定變形參數 (U = 常數) 定義的一平面與求解曲線的相交點決定,如下圖所示。
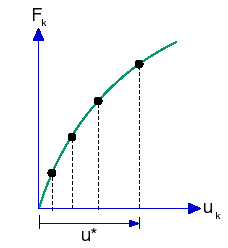
若要在有限元素分析納入此項技術,套用負載的模式為按比例增加 (使用單一負載乘數),以便在指定的自由度控制下達到平衡。控制的 DOF (以選擇頂點或參考點來指定) 會在使用的「時間」曲線期間漸增。
增量弧長控制方法
在此項策略中,使用拘束 (輔助) 方程式 (已加入控制系統平衡的方程式集) 來規定一個特殊參數。就幾何上來看,控制參數可視為平衡路徑上的「弧長」,如下圖所示。
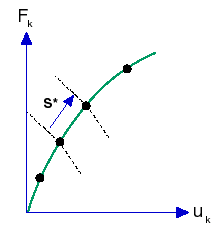
若要在有限元素分析使用此項技術,套用負載的模式為按比例增加 (使用單一負載乘數),以便在控制平衡路徑的指定長度 (弧長) 下達到平衡。程式會自動計算弧長。不需要「時間」曲線。
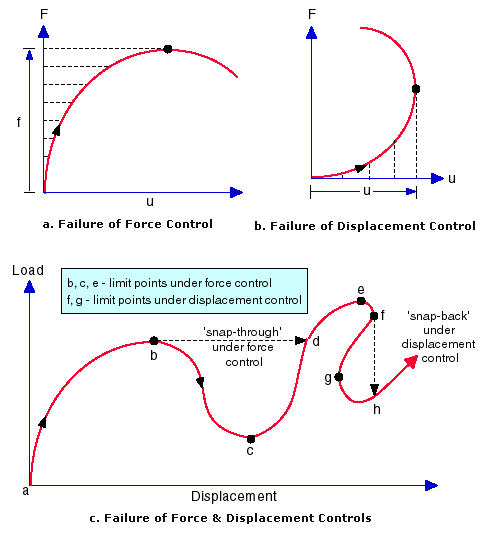
力控制及位移控制都會在轉折點附近失敗 (又稱為力控制的翹曲及位移控制的反向翹曲),如下圖所示。通常在框架、環及薄殼的挫曲分析中會遇到這些問題。弧長控制則可以成功克服這些問題。