Utilizzare l'analisi armonica per calcolare il responso più alto dello stato costante causato dai carichi armonici o le eccitazioni base.
Un carico armonico P viene espresso come P = A sin (ωt + φ) dove: A è l'ampiezza, ω è la frequenza, t il tempo e φ la fase angolare. Ecco di seguito gli esempi di carichi armonici con frequenze diverse w versus il tempo:
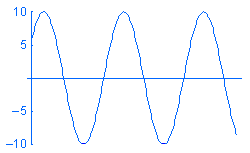
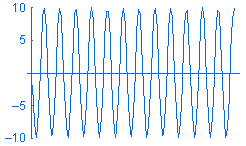
Sebbene sia possibile creare uno studio cronologico modale e definire i carichi come funzioni del tempo, potrebbe risultare poco interessante nella variazione transitoria del responso con il tempo. In questi casi, si risparmia del tempo e le risorse risolvendo per il responso elevato dello stato costante nel range di frequenze operative usando l'analisi armonica.
Per esempio, un motore montato su una tabella da test trasferisce carichi armonici al sistema di supporto attraverso i bulloni. Il sistema di supporto può essere modellato e uno studio armonico definito per valutare gli spostamenti elevati dello stato costante, le sollecitazioni, etc. per il range del motore delle frequenze operative. Il motore può essere approssimato per una massa distribuita.
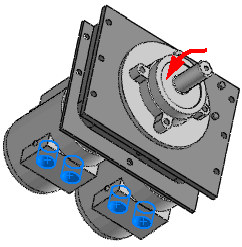
Dopo avere eseguito lo studio, è possibile visualizzare le sollecitazioni elevate, gli spostamenti, le accelerazioni e le velocità così come le fasi angolari del responso sul range delle frequenze operative.
Le opzioni di smorzamento modali, Rayleigh e composite sono disponibili per questo tipo di analisi.