El sistema de ecuaciones de movimiento de un sistema n grados de libertad excitado por una fuerza dependiente del tiempo es el siguiente:
(Ecuación 1)
donde:
[M] = n x n matriz de inercia simétrica
[C] = n x n matriz de amortiguamiento simétrico
[K] = n x n matriz de rigidez simétrica
{f(t)} = vector de fuerza de n dimensiones
, 
y 
son los vectores de n dimensiones de desplazamiento, velocidad y aceleración, respectivamente.
(Ecuación 1) es un sistema de n ecuaciones diferenciales normales simultáneas con coeficientes constantes. Las ecuaciones de movimiento están relacionadas a través de la masa, rigidez y amortiguamiento. La relación depende del sistema de coordenadas utilizado para describir las ecuaciones de movimiento matemáticamente.
La idea fundamental del análisis modal es transformar el sistema relacionado de (Ecuación 1) en un conjunto de ecuaciones independientes a través de la utilización de la matriz modal [Φ] como una matriz de transformación. [Φ] contiene los modos normales {f}i para i = 1, ....,n organizados de la siguiente forma:
(Ecuación 2)
Los modos normales y autovectores del sistema se derivan de la solución al problema de autovector:
(Ecuación 3)
donde [ω2] es la matriz diagonal de frecuencias cuadráticas naturales.
Para sistemas lineales, el sistema de n ecuaciones de movimiento puede desacoplarse en n ecuaciones de grados de libertad independientes en términos del vector de desplazamiento modal {x}:
(Ecuación 4)
Al sustituir el vector {u} de (Ecuación 4) y habiéndolo multiplicado previamente por [Φ]T (Ecuación 1) da como resultado:
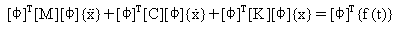(Ecuación 5)
Los modos normales satisfacen la propiedad de ortogonalidad y la matriz modal [Φ] se normaliza para cumplir con las siguientes ecuaciones:
(Ecuación 6)
(Ecuación 7) y
(Ecuación 8).
Al sustituir (Ecuación 6--8), (Ecuación 5) se convierte en el sistema de ecuaciones diferenciales de segundo orden con n SDOF independientes:
para i =1, ..., n (Ecuación 9)
(Ecuación 9) se soluciona mediante la utilización de métodos de integración paso a paso como el de Wilson-Theta y Newmark.
La integración se realiza en el dominio del tiempo, donde los resultados del último paso se utilizan para predecir los del siguiente.
El vector (u) de desplazamiento del sistema se deriva de (Ecuación 4).