En la teoría de la plasticidad de grandes deformaciones unitarias, una medida de deformación unitaria logarítmica se define como: 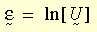
donde U es el tensor de estiramiento derecho que generalmente se obtiene de la descomposición polar derecha del gradiente de deformación F (es decir, F = R U; R es el tensor de rotación). La deformación unitaria logarítmica incremental se estima de la siguiente manera: 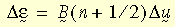
donde B(n+1/2) es la matriz de deformación unitaria-desplazamiento estimada en el paso de la solución n+1/2 y Δu es el vector de desplazamientos incrementales. Es preciso tener en cuenta que la forma anterior es una aproximación de segundo orden a la fórmula exacta.
La velocidad de tensión se toma de la velocidad de Green-Naghdi para que el modelo constitutivo sea objetivo y no produzca variaciones en las imágenes. Al transformar la velocidad de tensión del sistema global al sistema R:

El modelo constitutivo completo tendrá una forma idéntica a la teoría de pequeñas deformaciones unitarias. La teoría de plasticidad de grandes deformaciones unitarias se aplica al criterio de flexibilidad de von Mises, a la regla de flujo asociativo y al endurecimiento isotrópico o cinemático (bilineal o multilineal). El endurecimiento bilineal admite la dependencia de la temperatura de la propiedad de material. En el caso actual, se utiliza el algoritmo radial o de retorno. La idea básica consiste en aproximarse al vector normal N mediante:

donde 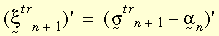
La siguiente figura ilustra las dos ecuaciones anteriores.
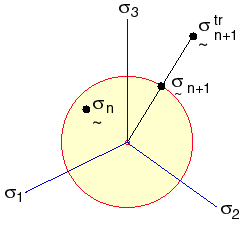
El vector de fuerza y las matrices de rigidez de los elementos se calculan según la fórmula lagrangiana actualizada. Las tensiones de Cauchy, las deformaciones unitarias logarítmicas y el espesor actual (sólo elementos de vaciado) se registran en el archivo de resultados.
La elasticidad en el caso actual se modela en una forma hiperelástica que supone la existencia de deformaciones unitarias elásticas pequeñas, pero admite deformaciones unitarias plásticas arbitrariamente grandes. Para problemas de elasticidad con deformaciones unitarias grandes (como el caucho), puede utilizar modelos de material hiperelástico como Mooney-Rivlin.
Debe utilizarse la tensión (verdadera) de Cauchy y la deformación unitaria logarítmica para la definición de la curva de tensión-deformación unitaria multilineal.