Contrariamente a lo que sucede con un material isotrópico, un material ortotrópico tiene direcciones preferidas de fuerza que son mutuamente perpendiculares. Las propiedades junto a estas direcciones (también conocidas como direcciones principales) son los valores extremos de coeficientes elásticos.
La matriz [D] para un material ortotrópico tiene nueve propiedades elásticas independientes. Además, hay tres propiedades para la expansión térmica.
Relaciones ortotrópicas de tensión-deformación unitaria en 2D
En dos dimensiones, las relaciones ortotrópicas de tensión-deformación unitaria pueden formularse de la siguiente manera, incluyendo los efectos de temperatura:
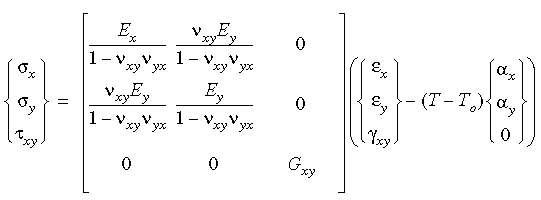
Observe que para satisfacer la simetría en la matriz de módulos elásticos, νxy Ey = νyx Ex.
Es necesario satisfacer la condición de simetría precedente al especificar los valores numéricos del módulo elástico o del coeficiente de Poisson.
Además, si no ingresa el valor numérico del módulo cortante, el programa lo calculará como se muestra a continuación:
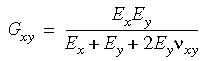
En tres dimensiones, las condiciones de simetría ortotrópicas dictan que:
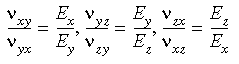
Al ingresar las propiedades de materiales ortotrópicos en tres dimensiones, debe asegurarse de que las condiciones de simetría anteriores no se infrinjan. Observe que si no ingresa los valores numéricos de módulos cortantes, el programa los calculará utilizando las relaciones que se muestran a continuación: 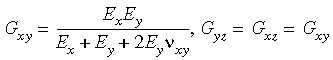
Si Ex = Ey = Ez, el programa calcula los módulos cortantes internamente aun si se han especificado explícitamente. El programa supone 0.0 para los coeficientes de Poisson que no se han definido explícitamente.