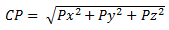| VON |
Von-Mises-Spannung |
| P1 |
Normalspannung in der ersten Hauptrichtung |
| P2 |
Normalspannung in der zweiten Hauptrichtung |
| P3 |
Normalspannung in der dritten Hauptrichtung |
| INT |
Spannungsintensität = P1 - P3 (a) Mit P1: absolute maximale Normalspannung und P3: Minimale absolute Normalspannung.
|
| TRI |
Triaxiale Spannung = P1 + P2 + P3 (Summe der Hauptspannungskomponenten. Diese werden auch als erste Spannungsinvariante bezeichnet, da sich der Wert nicht ändert, ganz gleich, welche Koordinatentransformation Sie auf den Spannungstensor anwenden.) |
| SX |
Normalspannung in die X-Richtung der ausgewählten Referenzgeometrie |
| SY |
Normalspannung in die Y-Richtung der ausgewählten Referenzgeometrie |
| SZ |
Normalspannung in die Z-Richtung der ausgewählten Referenzgeometrie |
| TXY |
Schubspannung in die Y-Richtung in der YZ-Ebene der ausgewählten Referenzgeometrie |
| TXZ |
Schubspannung in die Z-Richtung in der YZ-Ebene der ausgewählten Referenzgeometrie |
| TYZ |
Schubspannung in die Z-Richtung in der XZ-Ebene der ausgewählten Referenzgeometrie |
| ERR |
Energienormfehler |
| KD |
Kontaktdruck (b) |
| ILTXZ |
Interlaminarer Schub auf XZ-Ebene |
| ILTYZ |
Interlaminarer Schub auf YZ-Ebene |
(a) In einigen Konstruktionscodes und Referenzen wird die äquivalente Spannung (Tresca) durch den doppelten Wert der maximalen Schubspannung definiert. Dies entspricht (P1 – P3) oder andernfalls der Spannungsintensität.
(B) Kontaktdrücke werden durch Koordinatentransformation von den globalen Knotenspannungen abgeleitet. An jedem Knoten gibt der Solver die Kontaktkraft an. Wenn {Nx, Ny, Nz} der Einheitsvektor N entlang der Richtung der Kontaktkraft im globalen Koordinatensystem ist, wird der Knotenspannungstensor entlang des Einheitsvektors N projiziert, um die drei Komponenten des Kontaktdrucks {Px, Py, Pz} im globalen Koordinatensystem abzuleiten.
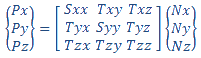
Die Größe des Kontaktdrucks CP an jedem Knoten ist die Quadratwurzel aus der Summe der Quadrate jeder Komponente. Die Richtung des Kontaktdrucks ist immer senkrecht zum Kontaktbereich.