Da Nitinol gewöhnlich wegen seiner Fähigkeit verwendet wird, endlichen Dehnungen ausgesetzt werden zu können, wird die Theorie für große Dehnungen unter Verwendung logarithmischer Dehnungen zusammen mit der aktualisierten Lagrange-Formel für dieses Modell benutzt.
Das konstitutive Modell wird also konstruiert, um die logarithmischen Dehnungen und die Kirchhoffschen Spannungskomponenten miteinander in Beziehung zu setzen. Schließlich werden die konstitutive Matrix und der Spannungsvektor jedoch transformiert, um die (wahren) Cauchy-Spannungen zu liefern.
|
σst1, σft1
|
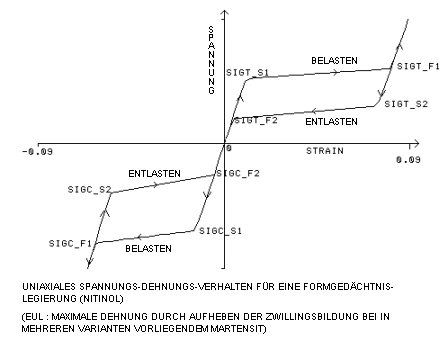
Anfängliche und endgültige Elastizitätsgrenze für Zugbelastung [SIGT_S1, SIGT_F1]
|
|
σst2, σft2
|
Anfängliche und endgültige Elastizitätsgrenze für Zugentlastung [SIGT_S2, SIGT_F2]
|
|
σsc1, σfc1
|
Anfängliche und endgültige Elastizitätsgrenze für Druckbelastung [SIGC_S1, SIGC_F1]
|
|
σsc2, σfc2
|
Anfängliche und endgültige Elastizitätsgrenze für Druckentlastung [SIGC_S2, SIGC_F2]
|
|
eul
|
(Maximale plastische Zugdehnung) *(3/2)0,5
|
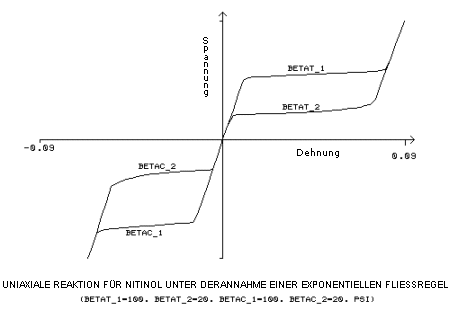
Die exponentielle Fließregel verwendet die zusätzlichen Eingabekonstanten β
t1, β
t2, β
c1, β
c2:
|
βt1
|
Materialparameter, misst die Geschwindigkeit der Transformation für Zugbelastung, [BETAT_1]
|
|
βt2
|
Materialparameter, misst die Geschwindigkeit der Transformation für Zugentlastung, [BETAT_2]
|
|
βc1
|
Materialparameter, misst die Geschwindigkeit der Transformation für Druckbelastung, [BETAC_1]
|
|
βc2
|
Materialparameter, misst die Geschwindigkeit der Transformation für Druckentlastung, [BETAC_2]
|
Das Fließkriterium
Zum Modellieren der Wahrscheinlichkeit der Druckabhängigkeit der Phasentransformation wird eine Belastungsfunktion vom Typ "Drucker-Prager" für das Fließkriterium verwendet:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RIf = 0
Dabei gilt Folgendes:
σ(bar) = Wirkspannung
p = Mittelspannung (oder hydrostatischer Druck)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 - σst1)
RfI = [ σfI(sqrt(2/3) + α)], I = 1 für Belastung und 2 für Entlastung