Dalla curva S-N di resistenza alla fatica di un determinato materiale, è possibile derivare le costanti dell'equazione di Basquin oppure consentirne il calcolo da parte del programma specificando il numero di punti dati sulla curva S-N da includere nei calcoli di adattamento della curva.
Alcuni materiali disponibili nel database dei materiali SOLIDWORKS e nel portale Web dei materiali SOLIDWORKS includono informazioni sui dati della curva S-N di fatica. Ad esempio, la curva S-N del materiale Ti-6AI-4V (lega a base di titanio con alluminio e vanadio) scaricata dal portale Web dei materiali SOLIDWORKS (il formato del database dei materiali è *.sldmat) è illustrata in scala log S - log N.
Nella tabella vengono forniti i valori numerici dei primi quattro punti dati S-N.

L'equazione di Basquin è un rapporto di legge di potenza che descrive la relazione lineare tra i cicli di sollecitazione (S) applicati nell'asse y e il numero di cicli necessari per provocare il cedimento nell'asse x rappresentata in una scala log-log.
Può essere definita come:

dove N è il numero di cicli necessari per provocare il cedimento, in genere maggiore di 104, Sr è il valore di riferimento della resistenza alla fatica (in Simulation si tratta dell'intervallo di sollecitazione ottenuto come 2* sollecitazione alternata), m è la pendenza della curva di resistenza alla fatica log s - log n e B è il valore della sollecitazione in un ciclo.
Per calcolare la pendenza m dell'equazione di Basquin, risolvere il sistema di equazioni:
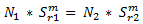
Per risolvere m, ricavare il log di entrambe le espressioni:

Sostituendo i primi due punti dati S-N dalla tabella precedente, calcolare prima m e quindi B:
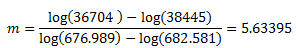

Per la costante B, il programma considera il valore dell'intervallo di sollecitazione (dalla sollecitazione ciclica massima alla sollecitazione ciclica minima). Se i valori di sollecitazione della curva S-N vengono forniti come sollecitazioni alternate (pratica comune), moltiplicare queste sollecitazioni per 2 per calcolare la costante B (intervallo di sollecitazione = 2* sollecitazione alternata, presupponendo una sollecitazione media pari a zero e l'inversione completa del carico ciclico). Se i dati della curva S-N vengono forniti in valori dell'intervallo di sollecitazione, applicarli direttamente nell'equazione per stimare la costante B. Per il calcolo della costante della pendenza m, la moltiplicazione delle sollecitazioni non altera il valore di pendenza.
Nella scheda
Curve SN fatica (finestra di dialogo
Materiale) immettere i valori di B in
Costante specifica della curva (B) e m in
Pendenza della curva S-N (m). Selezionare le unità appropriate di sollecitazione in
Unità e deselezionare
Stima costanti di Basquin dalla curva S-N.
È inoltre possibile trovare grafici di curve di resistenza alla fatica nei codici, tra cui Eurocode 9: Design of aluminum structures: Structures susceptible to fatigue, Ref. EN 1999-1-3:2007/A1.
Esempio di curva S-N di resistenza alla fatica
In Eurocode 9 è possibile trovare valori numerici per la pendenza della costante m per varie categorie di dettaglio e quindi calcolare B.
Ad esempio, in Ref. Table J.2 - Detail categories for plain members, EN 1999-1-3:2007/A1 per una semplice piastra con fori, l'intervallo di sollecitazione Ds = 100 MPa a N = 2x106 cicli e la pendenza m = 7, quindi B è uguale a:
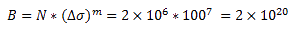
Per consentire al programma di eseguire l'adattamento della curva in un determinato set di dati S-N su una linea retta, selezionare Stima costanti di Basquin dalla curva S-N. In questo caso, accertarsi che Interpolare sia impostato su Log-log e selezionare l'ultimo punto dati S-N da considerare per l'adattamento della curva in Considera il punto di taglio per la curva S-N alla riga.
I due grafici mostrano la sovrapposizione di una curva S-N originale (linea rossa) con la linea di adattamento della curva dell'equazione di Basquin (linea verde) rispettivamente per 2 (A) e 22 (b) punti dati S-N. È consigliabile controllare la qualità dell'adattamento della curva di Basquin prima di procedere con l'analisi. La qualità della linea di adattamento della curva nell'approssimazione alla curva S-N originale è migliore per la porzione della curva S-N fino al punto di taglio.
 |
 |
| (a) Adattamento della curva di Basquin con 2 punti dati S-N (linea verde). |
(b) Adattamento della curva di Basquin con 22 punti dati S-N (linea verde). |