Оценка степени повреждения вследствие усталости материала для компонентов, работающих в среде случайных колебаний, производится в определенном диапазоне частот на основе статистических свойств реакции на напряжение функции спектральной плотности мощности (PSD).
Когда структуры или механические компоненты подвергаются воздействию нагрузок в форме случайных воздействий, например, в ветряной турбине при воздействии ветра, в береговой структуре при воздействии волн или в двигателе автомобиля, работающем в условиях разных профилей дорожного полотна, оценка срока службы при усталостных нагрузках выполняется в определенном диапазоне частот.
Термин вибрационная усталость (или усталость при вибрациях) относится к оценке срока службы при усталостных нагрузках, когда нагрузка и реакция (изменение напряжения во времени) являются случайными процессами, а следовательно, лучше всего описываются статистическими функциями, такими как функции спектральной плотности мощности (PSD).
Статистические характеристики реакции на напряжение PSD можно получить, рассматривая моментальные значения функции PSD.
| Статистические характеристики PSD |
Уравнение |
|---|
| Спектральный момент n напряжения PSD S(f) при частоте f (в герцах). |
 (Ур. 1) (Ур. 1)
|
| Среднеквадратичное значение для непрерывного стационарного гауссовского процесса . |
 (Ур. 2) (Ур. 2)
|
| Среднее число переходов через нулевое значение E[0] в направлении увеличения для типичного образца длительностью 1 секунда. |
 (Ур. 3) (Ур. 3)
|
| Среднее число пиковых значений E[p] для типичного образца длительностью 1 секунда. |
 (Ур. 4) (Ур. 4)
|
| Коэффициент неравномерности изменяется в пределах от 0 до 1. Он близок к 1, когда сигнал напряжения приближается к узкополосному процессу (для синусоиды =1). Он близок к 0, когда сигнал напряжения приближается к белому шуму. |
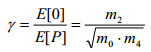 (Ур. 5) (Ур. 5)
или 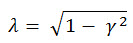 (Ур. 6) (Ур. 6)
|
Свойства усталости материала обычно получают из кривой S-N, которая описывает зависимость между диапазоном напряжения S (это отклонение напряжения от максимального циклического напряжения в состоянии натяжения до минимального циклического напряжения в состоянии сжатия) и средним количеством циклов до сбоя N.
Для большинства задач оценки многоцикловой усталости (N >= 104 ), кривую S-N можно выразить в упрощенной форме:
 (Ур. 7)
(Ур. 7)
где B и m — свойства материала, изменяющиеся в зависимости от нагрузки и условий среды, которые определяются в ходе испытаний на усталостное разрушение.
Оценка накопленного повреждения E[AD] в результате усталости от случайных нагрузок, основана на законе Палмгрена-Майнера и выражается как:
 (Ур. 8)
(Ур. 8)
где n(S) — число циклов воздействия на уровне диапазона напряжения S, p(S) — функция плотности распределения вероятности для этого диапазона напряжения. Подставляя выражение для упрощенной кривой S-N в вышеприведенное уравнение, можно получить общее уравнение, описывающее зависимость степени повреждения вследствие усталости материала от реакции на случайное напряжение:
 (Ур. 9), где T — продолжительность воздействия случайных нагрузок в секундах.
(Ур. 9), где T — продолжительность воздействия случайных нагрузок в секундах.
Существуют три метода для оценки степени повреждения вследствие усталости материала, основанные на Ур. 9: метод Штейнберга, метод узкого диапазона и метод окончательной обработки. В каждом методе используется свое определение функции плотности распределения вероятности p(S).
Метод узкого диапазона
В методе узкого диапазона, пиковые значения функции плотности распределения вероятности для сигнала в узком диапазоне соответствуют распределению Рэлея (Bendat J.S., Probability Functions for Random Responses. NASA report on Contact NASA-5-4590, 1964).
 (Ур. 10)
(Ур. 10)
Подставив (Ур. 10) в (Ур. 9) и проинтегрировав результаты мы получим следующее выражение для оценки степени повреждения вследствие усталости материала.
 (Ур. 11), где (.) — это Гамма функция.
(Ур. 11), где (.) — это Гамма функция.
Метод окончательной обработки
Метод окончательной обработки (Wirshing, P.H., Paez, T.L., and Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995) изменяет метод узкого диапазона, вводя эмпирический корректирующий коэффициент, позволяющий учесть широкополосный процесс.
 (Ур. 12)
(Ур. 12)
 (Ур. 13)
(Ур. 13)
w — эмпирический коэффициент, полученный с помощью моделирования методом Монте-Карло, который включает разные функции спектральной плотности.
w и bw – наиболее подходящие параметры, полученные из:
 (Ур. 14)
(Ур. 14)
Метод Штейнберга
В основе метода Штейнберга лежит допущение, что функция плотности распределения вероятности для случайных нагрузок соответствуют распределению Гаусса, и, следовательно, ожидаемые значения амплитуд реакции на напряжение ограничены определенными уровнями вероятности:
- 68,27% – вероятность того, что амплитуда циклов напряжения не выйдет за пределы диапазона, ограниченного 2-кратным среднеквадратичным значением сигнала реакции на напряжение.
- 27,1 % – вероятность того, что амплитуда циклов напряжения не выйдет за пределы диапазона, ограниченного 4-кратным среднеквадратичным значением сигнала реакции на напряжение.
- 4,3% – вероятность того, что амплитуда циклов напряжения не выйдет за пределы диапазона, ограниченного 6-кратным среднеквадратичным значением сигнала реакции на напряжение.
Для диапазонов, превышающих 6-кратное среднеквадратичное значение, циклов напряжения не происходит.
Ожидаемое значение степени повреждения вследствие усталости материала определяется выражением:
 (Ур. 15)
(Ур. 15)
В ПО Simulation, функции PSD напряжения являются результатом динамического исследования случайных колебаний, на котором основана оценка усталости. Компонент напряжения vonMises учитывается при расчете ожидаемого повреждения вследствие усталости во всех трех методах.