W teorii plastyczności dużego odkształcenia definiowana jest logarytmiczna miara odkształcenia jako: 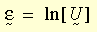
gdzie: U jest właściwym tensorem rozciągnięcia, zwykle uzyskiwanym z właściwego rozkładu biegunowego gradientu deformacji F (tj. F = R U, R jest tensorem obrotu). Przyrostowe odkształcenie logarytmiczne jest obliczane jako: 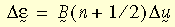
gdzie: B(n+1/2) jest macierzą odkształcenia-przemieszczenia obliczaną w kroku rozwiązania n+1/2, a Δu jest przyrostowym wektorem przemieszczeń. Należy zauważyć, że powyższa postać jest przybliżeniem drugiego stopnia dokładnego wzoru.
Natężenie naprężenia przyjęto jako natężenie Greena-Naghdiego, aby uzyskać prawidłową niezmienność lub obiektywność konstytucyjnego modelu. Poprzez transformację natężenia naprężenia z układu globalnego do układu R:
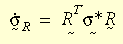
Cały model konstytucyjny przybierze identyczną postać jak w teorii małego odkształcenia. Teoria plastyczności dużego odkształcenia jest stosowana do kryterium ustępowania von Misesa, skojarzonej reguły płynięcia oraz izotropowego lub kinematycznego utwardzania (dwuliniowego lub wieloliniowego). Zależność właściwości materiału od temperatury materiału jest obsługiwana przez dwuliniowe utwardzanie. W bieżącym przypadku używany jest algorytm promieniowo-powrotny. Podstawową zasadą jest przybliżenie wektora normalnego N przez:

gdzie: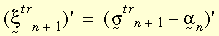
Poniższy rysunek ilustruje powyższe dwa równania.
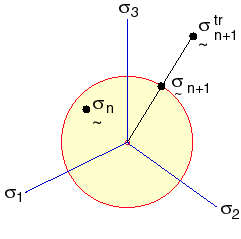
Wektor siły elementu i macierze sztywności są obliczane w oparciu o zaktualizowane wyrażenie Lagrange'a. Naprężenia Cauchy'ego, naprężenia logarytmiczne i bieżąca grubość (tylko w elementach skorupowych) są zapisywane w pliku wyjściowym.
Sprężystość w bieżącym przypadku jest modelowana w postaci hipersprężystej, która zakłada niewielkie odkształcenia elastyczne, lecz dopuszcza dowolnie duże odkształcenia plastyczne. W przypadku problemów sprężystych dużego odkształcenia można użyć hipersprężystych modeli materiału, takich jak Mooney-Rivlin.
Naprężenie Cauchy'ego (rzeczywiste) i naprężenie logarytmiczne należy użyć przy definiowaniu wieloliniowej krzywej rozciągania.