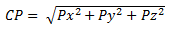| VON |
Tensão de von Mises |
| P1 |
tensão normal na primeira direção principal |
| P2 |
tensão normal na segunda direção principal |
| P3 |
tensão normal na terceira direção principal |
| INT: |
Intensidade da tensão = P1 - P3 (a) com P1: tensão normal máxima absoluta, e P3: tensão normal mínima absoluta.
|
| TRI |
Tensão triaxial = P1 + P2 + P3 (soma dos componentes de tensão principal. Também chamado de a primeira constante de tensão, pois o valor não muda qualquer que seja a transformação de coordenada aplicada ao tensor de tensão). |
| SX |
tensão normal na direção X da geometria de referência selecionada |
| SY |
tensão normal na direção Y da geometria de referência selecionada |
| SZ |
tensão normal na direção Z da geometria de referência selecionada |
| TXY |
tensão de cisalhamento na direção Y agindo no plano YZ da geometria de referência selecionada |
| TXZ |
tensão de cisalhamento na direção Z agindo no plano YZ da geometria de referência selecionada |
| TYZ |
tensão de cisalhamento na direção Z agindo no plano XZ da geometria de referência selecionada |
| ERR |
Erro de norma de energia |
| CP: |
Pressão de contato (b) |
| ILTXZ |
Cisalhamento interlaminar no plano XZ |
| ILTYZ |
Cisalhamento interlaminar no plano YZ |
(a) Em alguns códigos e referências de projetos, a tensão equivalente de Tresca é definida como duas vezes a tensão máxima de cisalhamento, que é igual a (P1 – P3) ou maior que a intensidade da tensão.
(b) As pressões de contato são derivadas das tensões nodais globais por transformação de coordenadas. Em cada nó, o solver relata a força de contato. Se o vetor de unidade N ao longo da direção da força de contato é {Nx, Ny, Nz} no sistema de coordenadas global, o tensor de tensão nodal é projetado ao longo do vetor de unidade N para derivar os três componentes de pressão de contato {Px, Py, Pz} no sistema de coordenadas global.
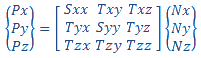
A magnitude da pressão de contato CP em cada nó é a raiz quadrada da soma dos quadrados de cada componente. A direção da pressão de contato é sempre normal à área de contato.